|
Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Задачи-4(10 класс)
Задачи
2. Даны точки А (1; 2; 3), В (0; 1; 2), С (0; 0; 3), D(l; 2; 0). Какие из этих точек лежат: 1) в плоскости ху; 2) на оси z; 3) в плоскости yz?
3. Дана точка А (1; 2; 3). Найдите основания перпендикуляров, опущенных из этой точки на координатные оси и координатные плоскости. 4. Найдите расстояния от точки (1; 2; —3) до: 1) координатных плоскостей; 2) осей координат; 3) начала координат.
5. В плоскости ху найдите точку D (х; у; 0), равноудаленную от трех данных точек: А (0; 1; —1), В( —1; 0; 1), С(0; -1; 0). 6. Найдите точки, равноотстоящие от точек (0; 0; 1), (0; 1; 0), (1; 0; 0) и отстоящие от плоскости yz на расстояние 2. 7. На оси X найдите точку С (х; 0; 0), равноудаленную от двух точек А (1; 2; 3), В ( — 2; 1; 3). 8. Составьте уравнение геометрического места точек пространства, равноудаленных от точки А (1; 2; 3) и начала координат. 9. Докажите, что четырехугольник ABCD с вершинами в точках А(1;2;3), В{0;2;4), С(1;1;4), D(2;2;2) является параллелограммом. 10. Докажите, что четырехугольник ABCD является параллелограммом, если: 1)А(0; 2; —3), В(—1; 1; 1), С(2; —2; -1),D(3; -1; -5); 2) А (2; 1; 3),В(1; 0; 7),С(-2; 1; 5), D(-1; 2; 1). 11. Докажите, что четырехугольник ABCD является ромбом, если: 1) А (6; 7; 8), В (8; 2; 6), С (4; 3; 2), D (2; 8; 4); 2) А (0; 2; 0), В(1; 0; 0), С (2; 0; 2), D (1; 2; 2).
12. Даны один конец отрезка А (2; 3; —1) и его середина С(1; 1; 1). Найдите второй конец отрезка В(х; у; z). 13. Найдите координаты вершины D параллелограмма ABCD, если координаты трех других его вершин известны: 1) А (2; 3; 2), В (0; 2; 4), С (4; 1; 0); 2) А (1; -1; 0), В(0; 1; -1),С(-1;0; 1); 3) А(4; 2; -1),В(1; -3; 2), С (-4; 2; 1).
14. Докажите, что середина отрезка с концами в точках А (a; с; —b) и В(—a; d; b) лежит на оси у. 15. Докажите, что середина отрезка с концами в точках С (a; b; с) и D (p;.q; —с) лежит в плоскости ху. 16. Докажите, что преобразование симметрии относительно координатной плоскости ху задается формулами х' = х, у' = у, z'=~z. 17. Даны точки (1; 2; 3), (0; — 1; 2), (1; 0; —3). Найдите точки, симметричные данным относительно координатных плоскостей. 18. Даны точки (1; 2; 3), (0; — 1; 2), (1; 0; —3). Найдите точки, симметричные им относительно начала координат. 19. Докажите, что преобразование симметрии относительно точки есть движение. 20*. Докажите, что преобразование симметрии относительно плоскости есть движение. 21. Докажите, что при движении в пространстве круг переходит в круг того же радиуса. 22. Докажите, что при движении в пространстве три точки, лежащие на прямой, переходят в три точки, также лежа-1цие на одной прямой. 23. Найдите значения а, b, с в формулах параллельного переноса х' = х + а, у' = у + b, z' = z + c, если при этом параллельном переносе точка A (1; 0; 2) переходит в точку А' (2; 1; 0). 24. При параллельном переносе точка А (2; 1; —1) переходит в точку А' (1; —1; 0). В какую точку переходит начало координат? 25. Существует ли параллельный перенос, при котором точка А переходит в точку В, а точка С — в точку D, если: 1) А(2;1;0), В(1; 0;1), С(3;-2;1), D(2;-3;0);
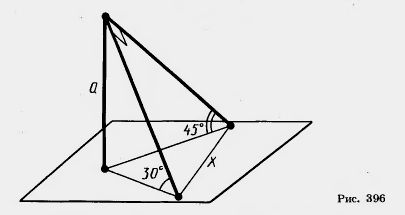
26. Докажите, что при параллельном переносе параллелограмм переходит в равный ему параллелограмм. 27. Четыре параллельные прямые пересекают параллельные плоскости в вершинах параллелограммов ABCD и A1B1C1D1 соответственно. Докажите, что параллелограммы ABCD и A1B1C1D1, совмещаются параллельным переносом. 28. Докажите, что преобразование гомотетии в пространстве является преобразованием подобия. 29. Три прямые, проходящие через точку S, пересекают данную плоскость в точках А, В, С, а параллельную ей плоскость в точках A1,B1,C1, Докажите, что треугольники ABC и A1B1C1 гомотетичны. 30. Прямая a лежит в плоскости 31*. Даны три точки А, В, С, не лежащие на одной прямой. Чему равен угол между прямыми СА и СВ, если эти прямые образуют углы 32. Прямые a, b, с параллельны одной и той же плоскости. Чему равен угол между прямыми b и с, если углы этих прямых с прямой a равны 60° и 80°? 33. Докажите, что любая прямая на плоскости, перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. 34. 1) Докажите, что прямая, пересекающая параллельные плоскости, пересекает их под равными углами. 35. Точка А отстоит от плоскости па расстояние h. Найдите длины наклонных, проведенных из этой точки под следующими углами к плоскости: 1) 30°; 2) 45°; 3) 60°. 36. Наклонная равна a. Чему равна проекция этой наклонной на плоскость, если наклонная составляет с плоскостью угол, равный: 1) 45°; 2) 60°; 3) 30°? 37. Отрезок длиной 10 м пересекает плоскость, концы его находятся на расстояниях 2 м и 3 м от плоскости. Найдите угол между данным отрезком и плоскостью. 38. Из точки, отстоящей от плоскости на расстояние a, проведены две наклонные, образующие с плоскостью углы 45° и 30°, а между собой прямой угол. Найдите расстояние между концами наклонных (рис. 396).
40. Из точки, отстоящей от плоскости на расстояние a, проведены две наклонные под углом 30° к плоскости, причем их проекции образуют угол 120°. Найдите расстояние между концами наклонных. 41. Через катет равнобедренного прямоугольного треугольника проведена плоскость под углом 45° ко второму катету. Найдите угол между гипотенузой и плоскостью. 42. Докажите, что плоскость, пересекающая параллельные плоскости, пересекает их под равными углами. 43. Две плоскости пересекаются под углом 30°. Точка А, лежащая в одной из этих плоскостей, отстоит от второй плоскости на расстояние a. Найдите расстояние от этой точки до прямой пересечения плоскостей. 44. Найдите угол между плоскостями, если точка, взятая на одной из них, отстоит от прямой пересечения плоскостей вдвое дальше, чем от второй плоскости. 45. Два равнобедренных треугольника имеют общее основание, а их плоскости образуют угол 60°. Общее основание равно 16 м, боковая сторона одного треугольника 17 м, а боковые стороны другого перпендикулярны. Найдите расстояние между вершинами треугольников. 46. Равнобедренные треугольники ABC и ABD с общим основанием АВ лежат в различных плоскостях, угол между которыми равен 1) ЛВ=24 см, АС= 13 см, AD = 37 см, CD = 35 см;
47. Катеты прямоугольного треугольника равны 7 м и 24 м. Найдите расстояние от вершины прямого угла до плоскости, которая проходит через гипотенузу и составляет угол 30° с плоскостью треугольника. 48. Дан равносторонний треугольник со стороной a. Найдите площадь его ортогональной проекции на плоскость, которая образует с плоскостью треугольника угол, равный: 1) 30°; 2) 45°; 3) 60°. 49. 1) Найдите площадь ортогональной проекции треугольника ABC из задачи 46 на плоскость треугольника ABD. 2) Найдите площадь ортогональной проекции треугольника ABD из задачи 46 на плоскость треугольника ABC. 50. Даны четыре точки А (2; 7; —3), В(1; 0; 3), С ( — 3; — 4; 5), D( — 2; 3; — 1). Укажите среди векторов 51. Даны три точки А (1; 0; 1), В( —1; 1; 2), C(0;2; —1). Найдите точку D(x; у; z), если векторы 52. Найдите точку D в задаче 51, если сумма векторов 53. Даны векторы 54. Дан вектор 55. При каком значении n данные векторы перпендикулярны:
56. Даны три точки А (1; 0; 1), В ( —1; 1; 2), С (0; 2; —1). Найдите на оси z такую точку D(0; 0; с), чтобы векторы 57*. Векторы 58*. Векторы 59. Даны четыре точки А (0; 1; —1), В(1; —1; 2), С (3; 1; 0), D (2; —3; 1), Найдите косинус угла 60. Даны три точки А (0; 1; —1), В(1; —1; 2), С(3; 1; 0). Найдите косинус угла С треугольника ABC. 62*. Из вершины прямого угла А треугольника ABC восставлен перпендикуляр AD к плоскости треугольника. Найдите косинус угла
64*. Из точки вне плоскости проведены перпендикуляр и две равные наклонные, образуюхцие углы
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: