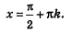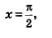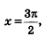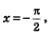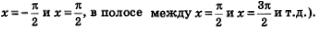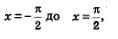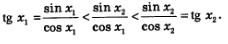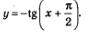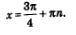|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Функции y = tgx, y = ctgx, их свойства и графики
§ 15. Функции y = tgx, y = ctgx, их свойства и графики
Отметим свойства функции у = tg х, причем в первую очередь те, которые помогут составить представление о графике функции (большинство из этих свойств фактически известно нам из § 5). Когда такое представление сложится, начнем строить график, как обычно, по точкам.
Свойство 1. Область определения функции у = tg х — множество всех действительных чисел, за исключением чисел вида
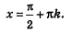
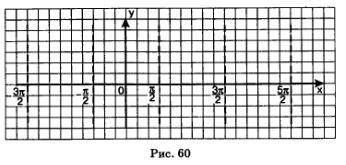
Это свойство означает, что на графике функции нет точки, принадлежащей прямой 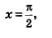 нет точки, принадлежащей прямой нет точки, принадлежащей прямой 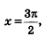 нет точки, принадлежащей прямой нет точки, принадлежащей прямой 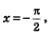 и т.д. Эти прямые проведены пунктиром на рис. 60. и т.д. Эти прямые проведены пунктиром на рис. 60.
Первое представление о графике получено: он состоит из бесконечного множества ветвей (в полосе между 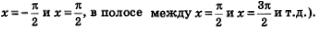
Свойство 2. у = tg х— периодическая функция с основным периодом п.
Это следует из двойного равенства 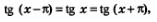 полученного в § 5. полученного в § 5.
Значит, если мы построим ветвь графика в полосе от 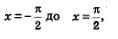 то затем нужно будет сдвинуть построенную ветвь по оси х вправо и влево на п, 2п, Зп и т.д. Тек самым получено второе представление о графике. то затем нужно будет сдвинуть построенную ветвь по оси х вправо и влево на п, 2п, Зп и т.д. Тек самым получено второе представление о графике.
Свойство 3. у =tg х—нечетная функция. Это следует из доказанного в § 5 соотношения 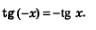 График нечетной функции симметричен относительно начала координат. Значит, нам можно действовать так: построить по точкам часть графика на промежутке от График нечетной функции симметричен относительно начала координат. Значит, нам можно действовать так: построить по точкам часть графика на промежутке от 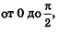 а затем воспользоваться указанной симметрией. а затем воспользоваться указанной симметрией.
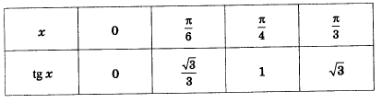
Приступим к построению графика на полуинтервале 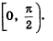 , Выберем контрольные точки: , Выберем контрольные точки:
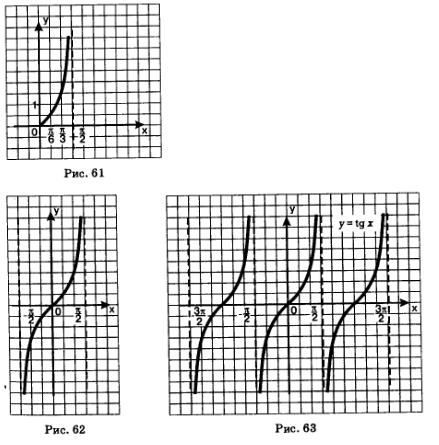
Отметим эти точки на координатной плоскости и проведем через них плавную кривую (рис. 61). Добавим линию, симметричную построенной кривой относительно начала координат (рис. 62). Воспользовавшись периодичностью, достроим график до конца (рис. 63).
График функции у = tg х называют тангенсоидой. Ту ее часть, которая изображена на рис. 62, обычно называют главной ветвью тангенсоиды.
Обратите внимание на то, что из начала координат главная ветвь тангенсоиды выходит как бы под углом 45°. Почему это так, вы узнаете из главы 4.
Свойство 4. Функция возрастает на интервале 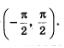 В более общем виде — функция возрастает на любом интервале вида В более общем виде — функция возрастает на любом интервале вида 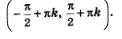
Свойство 5. Функция у = tg хне ограничена ни сверху, ни снизу.
Свойство 6. У функции у = tg х нет ни наибольшего, ни наимень шего значения.
Свойство 7. Функция у = tg х непрерывна на интервале 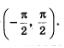 В более общем виде — функция непрерывна на любом интервале вида В более общем виде — функция непрерывна на любом интервале вида 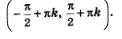
При значениях 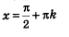 функция претерпевает разрыв. Каждая прямая вида функция претерпевает разрыв. Каждая прямая вида 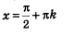 служит вертикальной асимптотои графика функции. служит вертикальной асимптотои графика функции.
Свойство 8. 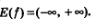
Замечание. Свойства 4—8, прочитанные по графику, можно доказать, опираясь на соответствующие математические утверждения, которые нам с вами пока не известны (поэтому мы и ограничиваемся наглядно-интуитивными представлениями). Впрочем, доказательство одного из свойств мы можем осуществить и сейчас.
Докажем, что функция у=tg х возрастает на полуинтервале 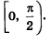 . Возьмем два значения аргумента х1 и х2 из этого промежутка: х1 < х2. Тогда в силу возрастания функции х на выбранном полуинтервале, будем иметь sin х1 < sin х2. В силу убывания функции у— соs х на выбранном полуинтервале будем иметь соs х1 > соs х2. Значит, . Возьмем два значения аргумента х1 и х2 из этого промежутка: х1 < х2. Тогда в силу возрастания функции х на выбранном полуинтервале, будем иметь sin х1 < sin х2. В силу убывания функции у— соs х на выбранном полуинтервале будем иметь соs х1 > соs х2. Значит,
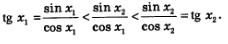
Итак, 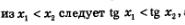 а это и означает возрастание функции у=tg х на выбранном промежутке. а это и означает возрастание функции у=tg х на выбранном промежутке.
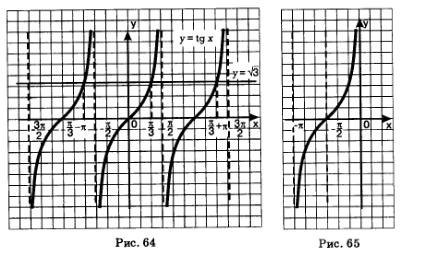
Пример 1. Решить уравнение tg х = 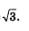
Решение. Построим в одной системе координат графики функций у =tg х — тангенсоиду и у = 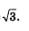 — прямую, параллельную оси х. Они имеют бесконечно много точек пересечения (рис. 64), причем абсциссы этих точек отличаются друг от друга на пк. На главной ветви абсцисса соответствующей точки равна — прямую, параллельную оси х. Они имеют бесконечно много точек пересечения (рис. 64), причем абсциссы этих точек отличаются друг от друга на пк. На главной ветви абсцисса соответствующей точки равна 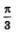 (мы воспользовались известным числовым равенством — (мы воспользовались известным числовым равенством — 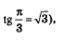 это один корень уравнения, а все решения описываются формулой это один корень уравнения, а все решения описываются формулой 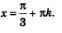
Ответ: 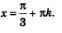
Пример 2. Построить график функции 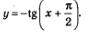
Решение. Для начала разберемся с главной ветвью тангенсоиды.
1) Перейдем к вспомогательной системе координат с началом в точке 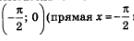 проведена на рис. 65 пунктиром). проведена на рис. 65 пунктиром).
2) "Привяжем" функцию у = tg хк новой системе координат — это будет график функции 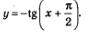 , а точнее, главная ветвь искомого графика (рис. 65 — сплошная кривая). , а точнее, главная ветвь искомого графика (рис. 65 — сплошная кривая).
3) Чтобы получить график функции 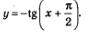 достаточно построенную ветвь отобразить симметрично относительно оси х (рис. 66). достаточно построенную ветвь отобразить симметрично относительно оси х (рис. 66).
4) Зная одну ветвь, можно построить весь график (рис. 67).
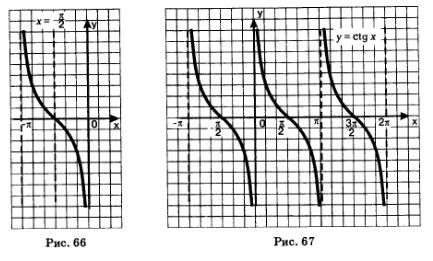
На самом деле, на рис. 67 построен график функции у=сtgх. Почему? Потому, что имеет место тождество (формула приведения) 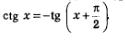
График функции у=сtg х, как и график функции у =tg х, называют тангенсоидой. Главной ветвью графика функции у=сtg х обычно называют ветвь, заключенную в полосе от х=0 до х = к.
Пример 3. Решить уравнение сtg х = -1.
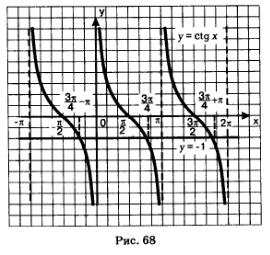
Решение. Построим в одной системе координат графики функций у = сtg х — тангенсоиду и у=-1 — прямую, параллельную оси х. Они имеют бесконечно много точек пересечения (рис. 68), причем абсциссы этих точек отличаются друг от друга на яп. На главной ветви абсцисса соответствующеи точки равна 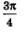 (мы воспользовались известным соотношением: (мы воспользовались известным соотношением: 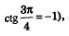 а все решения заданного уравнения можно охватить формулой а все решения заданного уравнения можно охватить формулой 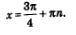
Ответ: 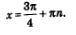
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|