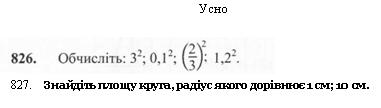|
|
|
| Строка 1: |
Строка 1: |
| - | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика]]>>[[Математика 6 клас|Математика 6 клас]]>> Математика: Тема 4.ВІДНОШЕННЯ І ПРОПОРЦІЇ .Круг. Площа круга ''' | + | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика]]>>[[Математика 6 клас|Математика 6 клас]]>>Круг. Площа круга ''' |
| | + | |
| | | | |
| | Кожне коло розбиває площину, на якій воно накреслене, на дві частини — внутрішню і зовнішню. Точки кола й усі внутрішні точки утворюють круг (рис. 12). Центр, радіус і діаметр кола називають відповідно центром, радіусом і діаметром цього круга.<br> | | Кожне коло розбиває площину, на якій воно накреслене, на дві частини — внутрішню і зовнішню. Точки кола й усі внутрішні точки утворюють круг (рис. 12). Центр, радіус і діаметр кола називають відповідно центром, радіусом і діаметром цього круга.<br> |
| | | | |
| - | [[Image:Asd210.jpg]]
| |
| | | | |
| - | Два радіуси ОА й ОБ розбивають круг на дві частини, кожну з яких нази-вають сектором. Будь-який діаметр розбиває круг на дві рівні частини, які нази-вають півкругами.<br><br>Практична робота<br>Тема роботи. Площа круга.<br>Обладнання. Циркуль, лінійка, аркуш паперу в клітинку.<br><br>Хід роботи<br>1. На аркуші паперу у клітинку будуємо коло, радіус якого дорівнює 4 см (8 клітинок).<br>[[Image:Asd211.jpg]]<br>
| |
| | | | |
| - | 3. Рахуємо кількість клітинок усередині контуру.<br>4. Рахуємо кількість клітинок зовні контуру, які частково належать кругу, й одержане число ділимо на 2 (у середньому частини двох неповних клітинок дають одну цілу).<br>5. Додаємо до числа клітинок, які повністю належать кругу, число, одержане в п. 4.<br>6. Оскільки площа 4 клітинок дорівнює 1 см2, то щоб виразити площу круга у квадратних сантиметрах, ділимо число, отримане в п. 5, на 4. Одержуємо наближене значення плоші: 5~ ... .<br>[[Image:Asd212.jpg]]
| + | [[Image:Asd210.jpg|Площа круга ]] |
| | | | |
| - | Прочитайте<br><br>1. Знайти площу круга, радіус якого дорівнює 1,5 см. •S= ПR<sup>2</sup>~ 3,14 • 1,5<sup>2</sup>= 3,14 • 2,25 = 7,065 (см2). •<br>[[Image:Asd213.jpg]]
| + | Два радіуси ОА й ОБ розбивають круг на дві частини, кожну з яких нази-вають сектором. Будь-який діаметр розбиває круг на дві рівні частини, які '''називають півкругами'''.<br><br>[[43._Практична_робота:_9._Опис_одного_з_головних_типів_клімату_за_кліматичними_картами.|'''Практична робота''']]<br>Тема роботи. Площа круга.<br>Обладнання. Циркуль, лінійка, аркуш паперу в клітинку.<br><br>'''Хід роботи'''<br>1. На аркуші паперу у клітинку будуємо коло, радіус якого дорівнює 4 см (8 клітинок). |
| | | | |
| - | Знайдіть площу круга:<br>828. а) радіус якого дорівнює 5 см; 11 см; 0,3 дм; б) діаметр якого дорівнює 0,6 м; 7 м.<br> <br>829.<br> <br>а) радіус якого дорівнює 8 см; 14 дм; 2,5 м;<br>б) діаметр якого дорівнює 1,6 м; 5 дм.<br><br>830. Зробіть необхідні вимірювання та знайдіть площі фігур, зображених на рисунку 14 а)-г).<br> <br>831. Зробіть необхідні вимірювання та знайдіть площі фігур, зображених на рисунку 14 д), е).<br><br> [[Image:Asd214.jpg]]<br>
| + | <br>[[Image:Asd211.jpg|Хід роботи]]<br> |
| | | | |
| - | Рівень Б<br><br><br>832. Довжина кола арени цирку дорівнює 47,1 м. Знайдіть площу арени (результат округліть до одиниць м<sup>2</sup>).<br> <br>833. Знайдіть площу круга, якщо довжина його кола дорівнює 25,12 см.<br> <br>834. Дано круг із центром О, радіус якого дорівнює 12 см (рис. 15). Знайдіть площу заштрихованого сектора, якщо він становить шосту частину круга.<br>835. У скільки разів збільшиться площа круга, якщо його радіус збільшити втричі?<br>[[Image:Asd215.jpg]]<br>
| + | 3. Рахуємо кількість клітинок усередині контуру.<br>4. Рахуємо кількість клітинок зовні контуру, які частково належать кругу, й одержане число ділимо на 2 (у середньому частини двох неповних клітинок дають одну цілу).<br>5. Додаємо до числа клітинок, які повністю належать кругу, число, одержане в п. 4.<br>6. Оскільки площа 4 клітинок дорівнює 1 см2, то щоб виразити площу круга у квадратних [[Порівняння_виразів_із_застосуванням_знаків_«більше»_і_«менше»._Поняття_«сантиметр»,_«дециметр»,_«метр»._Вимірювання_метром|сантиметр]]ах, ділимо число, отримане в п. 5, на 4. Одержуємо наближене значення плоші: 5~ ... . |
| | | | |
| - | 837. З аркуша квадратної форми зі стороною 0,6 м потрібно вирізати круг найбільшого радіуса. Чому дорівнює площа цього круга (результат округліть до сотих м<sup>2</sup>)?<br> <br>838. Діагональ квадрата дорівнює 20 см. Квадрат потрібно покрити кругом найменшого радіуса. Чому дорівнює площа цього круга?<br> <br>Потрібно зафарбувати круг, радіус якого дорівнює 3 м. Скільки потрібно для цього фарби, якщо на кожний квадратний метр витрачається 120 г фарби (результат округліть до десятків грамів)?<br> <br>Здогадайтеся<br> Вправи для повторення
| + | <br>[[Image:Asd212.jpg]] |
| | + | |
| | + | |
| | + | |
| | + | '''Прочитайте'''<br>1. Знайти площу круга, радіус якого дорівнює 1,5 см. •S= ПR<sup>2</sup>~ 3,14 • 1,5<sup>2</sup>= 3,14 • 2,25 = 7,065 (см2). •<br>[[Image:Asd213.jpg|Усні вправи]] |
| | + | |
| | + | Знайдіть площу круга:<br>828. а) радіус якого дорівнює 5 см; 11 см; 0,3 дм; б) діаметр якого дорівнює 0,6 м; 7 м.<br> <br>829. а) радіус якого дорівнює 8 см; 14 дм; 2,5 м;<br>б) діаметр якого дорівнює 1,6 м; 5 дм.<br><br>830. Зробіть необхідні вимірювання та знайдіть площі фігур, зображених на рисунку 14 а)-г).<br> <br>831. Зробіть необхідні вимірювання та знайдіть площі фігур, зображених на рисунку 14 д), е).<br><br> [[Image:Asd214.jpg|Зробіть вимірювання]]<br> |
| | + | |
| | + | |
| | + | |
| | + | '''Рівень Б'''<br>832. Довжина кола арени цирку дорівнює 47,1 м. Знайдіть площу арени (результат округліть до одиниць м<sup>2</sup>).<br> <br>833. Знайдіть площу круга, якщо довжина його кола дорівнює 25,12 см.<br> <br>834. Дано круг із центром О, радіус якого дорівнює 12 см (рис. 15). Знайдіть площу заштрихованого сектора, якщо він становить шосту частину [[Задачі_до_уроку:_Круг._Площа_круга|круг]]а. |
| | + | |
| | + | <br>835. У скільки разів збільшиться площа круга, якщо його радіус збільшити втричі? |
| | + | |
| | + | <br>[[Image:Asd215.jpg|площа круга]]<br> |
| | + | |
| | + | 837. З аркуша квадратної форми зі стороною 0,6 м потрібно вирізати круг найбільшого радіуса. Чому дорівнює площа цього круга (результат округліть до сотих м<sup>2</sup>)?<br> <br>838. [[Відеоматеріал_до_теми_«Класифікація_комбінацій_за_ідеями._Відкриття_вертикалі,_горизонталі_та_діагоналі»|Діагональ]] квадрата дорівнює 20 см. Квадрат потрібно покрити кругом найменшого радіуса. Чому дорівнює площа цього круга?<br> <br>Потрібно зафарбувати круг, радіус якого дорівнює 3 м. Скільки потрібно для цього фарби, якщо на кожний квадратний метр витрачається 120 г фарби (результат округліть до десятків грамів)?<br> <br>'''Вправи для повторення''' |
| | | | |
| | <br> | | <br> |
| | | | |
| - | [[Image:Asd216.jpg]]<br>[[Image:Asd217.jpg]]<br> | + | [[Image:Asd216.jpg|Вправи для повторення ]]<br>[[Image:Asd217.jpg]]<br> |
| | | | |
| | [[Image:Asd218.jpg]] | | [[Image:Asd218.jpg]] |
| | | | |
| - | [[Image:Asd219.jpg]]<br> | + | [[Image:Asd219.jpg|Вправи для повторення ]]<br> |
| | + | |
| | + | [[Математика_6_клас|<br>]] ''[[Математика_6_клас|Математика 6 клас]] Галина Янченко, Василь Кравчук '' |
| | + | |
| | + | ''Вислано читачами iнтернет-сайту '' |
| | + | |
| | | | |
| - | <br> <br> <sub>[[Гіпермаркет Знань - перший в світі!|Онлайн-бібліотека з підручниками]] і книгами, тести [[Математика|з математики]], завдання [[Математика 6 клас|з математики 6 клас]], календарне планування</sub><br> Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту
| |
| | | | |
| - | '''<u>Зміст уроку</u>'''
| + | <br> <sub>[[Гіпермаркет Знань - перший в світі!|Онлайн-бібліотека з підручниками]] і книгами, тести [[Математика|з математики]], завдання [[Математика 6 клас|з математики 6 клас]], календарне планування</sub> |
| | | | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B2%D0%B8%D1%87%D0%B0%D0%B9%D0%BD%D0%B8%D1%85_%D0%B4%D1%80%D0%BE%D0%B1%D1%96%D0%B2._%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D1%83_%D1%96_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%B8%D0%B9_%D0%BA%D0%B0%D1%80%D0%BA%D0%B0%D1%81 конспект уроку і опорний каркас] | + | '''<u>Зміст уроку |
| | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B2%D0%B8%D1%87%D0%B0%D0%B9%D0%BD%D0%B8%D1%85_%D0%B4%D1%80%D0%BE%D0%B1%D1%96%D0%B2._%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D1%83_%D1%96_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%B8%D0%B9_%D0%BA%D0%B0%D1%80%D0%BA%D0%B0%D1%81 конспект уроку і опорний каркас] |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентація уроку | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентація уроку |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративні методи та інтерактивні технології | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративні методи та інтерактивні технології |
Текущая версия на 09:13, 2 ноября 2012
Гіпермаркет Знань>>Математика>>Математика 6 клас>>Круг. Площа круга
Кожне коло розбиває площину, на якій воно накреслене, на дві частини — внутрішню і зовнішню. Точки кола й усі внутрішні точки утворюють круг (рис. 12). Центр, радіус і діаметр кола називають відповідно центром, радіусом і діаметром цього круга.
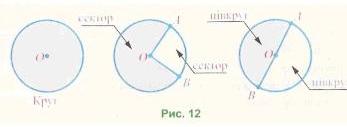
Два радіуси ОА й ОБ розбивають круг на дві частини, кожну з яких нази-вають сектором. Будь-який діаметр розбиває круг на дві рівні частини, які називають півкругами.
Практична робота
Тема роботи. Площа круга.
Обладнання. Циркуль, лінійка, аркуш паперу в клітинку.
Хід роботи
1. На аркуші паперу у клітинку будуємо коло, радіус якого дорівнює 4 см (8 клітинок).
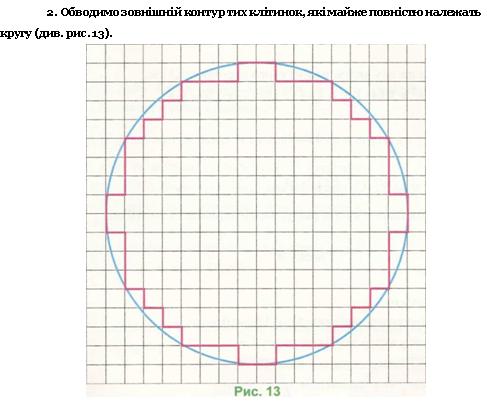
3. Рахуємо кількість клітинок усередині контуру.
4. Рахуємо кількість клітинок зовні контуру, які частково належать кругу, й одержане число ділимо на 2 (у середньому частини двох неповних клітинок дають одну цілу).
5. Додаємо до числа клітинок, які повністю належать кругу, число, одержане в п. 4.
6. Оскільки площа 4 клітинок дорівнює 1 см2, то щоб виразити площу круга у квадратних сантиметрах, ділимо число, отримане в п. 5, на 4. Одержуємо наближене значення плоші: 5~ ... .

Прочитайте
1. Знайти площу круга, радіус якого дорівнює 1,5 см. •S= ПR2~ 3,14 • 1,52= 3,14 • 2,25 = 7,065 (см2). •
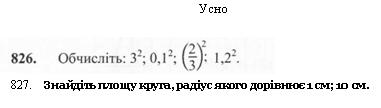
Знайдіть площу круга:
828. а) радіус якого дорівнює 5 см; 11 см; 0,3 дм; б) діаметр якого дорівнює 0,6 м; 7 м.
829. а) радіус якого дорівнює 8 см; 14 дм; 2,5 м;
б) діаметр якого дорівнює 1,6 м; 5 дм.
830. Зробіть необхідні вимірювання та знайдіть площі фігур, зображених на рисунку 14 а)-г).
831. Зробіть необхідні вимірювання та знайдіть площі фігур, зображених на рисунку 14 д), е).
Рівень Б
832. Довжина кола арени цирку дорівнює 47,1 м. Знайдіть площу арени (результат округліть до одиниць м2).
833. Знайдіть площу круга, якщо довжина його кола дорівнює 25,12 см.
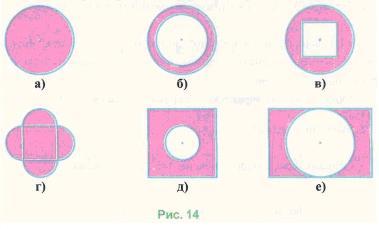
834. Дано круг із центром О, радіус якого дорівнює 12 см (рис. 15). Знайдіть площу заштрихованого сектора, якщо він становить шосту частину круга.
835. У скільки разів збільшиться площа круга, якщо його радіус збільшити втричі?
837. З аркуша квадратної форми зі стороною 0,6 м потрібно вирізати круг найбільшого радіуса. Чому дорівнює площа цього круга (результат округліть до сотих м2)?
838. Діагональ квадрата дорівнює 20 см. Квадрат потрібно покрити кругом найменшого радіуса. Чому дорівнює площа цього круга?
Потрібно зафарбувати круг, радіус якого дорівнює 3 м. Скільки потрібно для цього фарби, якщо на кожний квадратний метр витрачається 120 г фарби (результат округліть до десятків грамів)?
Вправи для повторення


Математика 6 клас Галина Янченко, Василь Кравчук
Вислано читачами iнтернет-сайту
Онлайн-бібліотека з підручниками і книгами, тести з математики, завдання з математики 6 клас, календарне планування
Зміст уроку
 конспект уроку і опорний каркас конспект уроку і опорний каркас
 презентація уроку презентація уроку
 акселеративні методи та інтерактивні технології акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями) закриті вправи (тільки для використання вчителями)
 оцінювання
Практика оцінювання
Практика
 задачі та вправи,самоперевірка задачі та вправи,самоперевірка
 практикуми, лабораторні, кейси практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання
Ілюстрації домашнє завдання
Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати реферати
 фішки для допитливих фішки для допитливих
 шпаргалки шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення
 зовнішнє незалежне тестування (ЗНТ) зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні підручники основні і допоміжні
 тематичні свята, девізи тематичні свята, девізи
 статті статті
 національні особливості національні особливості
 словник термінів словник термінів
 інше
Тільки для вчителів інше
Тільки для вчителів
 ідеальні уроки ідеальні уроки
 календарний план на рік календарний план на рік
 методичні рекомендації методичні рекомендації
 програми програми
 обговорення обговорення
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|