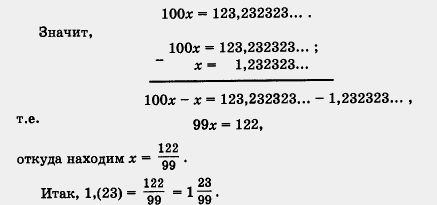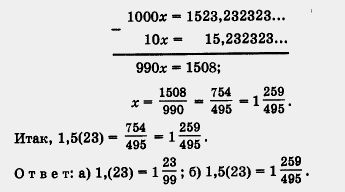Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Множество рациональных чисел

Множество рациональных чисел

В главе 3 мы убедились в том, что, кроме рациональных чисел, существуют числа другой природы — к ним часто приводит операция извлечения квадратного корня (и не только она, просто мы с вами этого пока не знаем). Значит, нам нужно более обстоятельно познакомиться с новыми числами. Но сначала попробуем систематизировать наши знания о «старых», т. е. о рациональных, числах.

1. Некоторые символы математического языка

Вам хорошо известны натуральные числа: 1, 2, 3, 4, ...

Множество всех натуральных чисел обычно обозначают буквой N.

Если к натуральным числам присоединить число 0 и все целые отрицательные числа: -1,-2,-3,-4, ..., — то получится множество целых чисел. Это множество обычно обозначают буквой Z.

Если к множеству целых чисел присоединить все обыкновенные дроби: и т. д., — то получится множество рациональных чисел. Это множество обычно обозначают буквой Q.

Любое целое число m можно записать в виде дроби , поэтому справедливо утверждение о том, что множество Q рациональных чисел — это ножество,  состоящее из чисел вида
Используя введенные обозначения N, Z, Q, условимся о следующем:

1. Вместо фразы «n — натуральное число» можно писать (читается: «элемент n принадлежит множеству N»), Математический символ называют знаком принадлежности.
2. Вместо фразы «m — целое число» можно писать m Z.
3. Вместо фразы «r — рациональное число» можно писать rQ.
Понятно, что N — часть множества Z, а Z — часть множества Q. Для описания этой ситуации в математике также имеется специальное обозначение:

Математический символ с называют знаком включения (одного множества в другое).

Вообще, в математике запись х X означает, что х — один из элементов множества X. Запись означает, что множество А представляет собой часть множества В. Математики чаще говорят так: А — подмножество множества

Обратите внимание: множества в математике обычно обозначают прописными буквами, а элементы множества — строчными буквами.

И еще на один момент обратите внимание: знаки принадлежности (элемент принадлежит множеству) и включения (одно множество содержится в другом) — различные, соответственно

А как записать, что элемент х не принадлежит множеству X или что множество А не является частью (подмножеством) множества В? Используют те же символы, но перечеркнутые косой чертой: .

Приведем несколько примеров использования введенных математических символов для сокращения записи верных математических утверждений — их называют также истинными высказываниями.

2. Рациональные числа как бесконечные десятичные периодические дроби

К рациональным числам, как мы уже не раз подчеркивали, относятся все те числа, с которыми вы успешно оперировали до тех пор, пока не встретились с квадратными корнями.

Это были целые числа, обыкновенные дроби, десятичные дроби.

Для всех этих чисел можно использовать один и тот же способ записи, который мы сейчас и обсудим.
Рассмотрим, например, целое число 5, обыкновенную дробь  и десятичную дробь 8,377. Целое число 5 можно записать в виде бесконечной десятичной дроби: 5,0000... Десятичную дробь 8,377 также можно записать в виде бесконечной десятичной дроби: 8,377000... Для числа воспользуемся методом «деления углом»:

Как видите, начиная со второй цифры после запятой происходит повторение одной и той же группы цифр: 18, 18, 18, ... . Таким образом, = 0,3181818... . Короче это записывают так: 0,3(18). Повторяющуюся группу цифр после запятой называют периодом, а саму десятичную дробь — бесконечной десятичной периодической дробью.
бесконечной десятичной периодической дроби. Для этого надо в периоде записать число 0:

5 = 5,00000... = 5,(0). Так же обстоит дело и с числом 8,377: 8,377 = 8,377000... = 8,377(0).

Чтобы все было аккуратно, говорят так: 8,377 — конечная десятичная дробь, а 8,377000... — бесконечная десятичная дробь.
Таким образом, и число 5, и число , и число 8,377 удалось записать в виде бесконечной десятичной периодической дроби.

Вообще, любое рациональное число можно записать в виде бесконечной десятичной периодической дроби.

Замечание. Этот вывод удобен для теории, но не очень удобен для практики. Ведь если дана конечная десятичная дробь 8,377, то зачем нужна ее запись в виде 8,377(0)? Поэтому обычно говорят так: любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби.

Выше мы показали, как обыкновенную дробь представляют в виде бесконечной периодической десятичной дроби. Верно и обратное: любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби. Это значит, что любая бесконечная десятичная периодическая дробь есть
рациональное число.

Покажем на примере, как бесконечную десятичную периодическую дробь превращают в обыкновенную дробь.

Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь: а) 1,(23); б) 1,5(23).

Решение, а) Положим х = 1,(23), т. е. х = 1,232323... .

Умножим х на такое число, чтобы запятая передвинулась вправо ровно на один период. Поскольку в периоде содержатся две цифры, нужно, чтобы запятая передвинулась вправо на две цифры, а для этого число х надо умножить на 100.

Получим

б) Положим х = 1,5(23) = 1,5232323... . Сначала умножим х на 10, чтобы в полученном произведении период начинался сразу после запятой: 10х = 15,232323... . Теперь число 10х умножим на 100 — тогда запятая сместится ровно на один период вправо: 1000х - 1523,232323... . Имеем

Теперь мы сформулируем основной результат этого параграфа: множество Q рациональных чисел можно рассматривать как множество чисел вида ,где m — целое число, n — натуральное число, или как множество бесконечных десятичных периодических дробей.

Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.