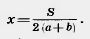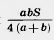Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Объем наклонного параллелепипеда

Объем наклонного параллелепипеда

Найдем объем наклонного параллелепипеда ABCDA₁B₁C₁D₁(рис. 476).

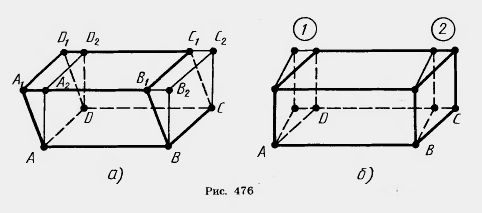
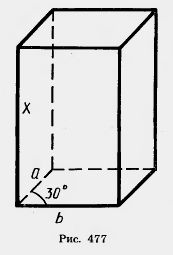
Проведем через ребро ВС плоскость, перпендикулярную основанию ABCD, и дополним наклонный параллелепипед треугольной призмой BB₁B₂CC₁C₂ (рис. 476, а). Отсечем теперь от  полученного тела треугольную призму плоскостью, проходящей через ребро AD и перпендикулярной основанию ABCD. Тогда получим снова параллелепипед. Этот параллелепипед имеет объем, равный объему исходного параллелепипеда.

Действительно, достроенная призма и отсекаемая совмещаются параллельным переносом на отрезок АВ, следовательно, имеют одинаковые объемы. При описанном преобразовании параллелепипеда сохраняются площадь его основания и высота. Сохраняются также плоскости двух боковых граней, а две другие становятся перпендикулярными основанию.

Применяя еще раз такое преобразование к наклонным граням, получим параллелепипед, у которого все боковые грани перпендикулярны основанию, т. е. прямой параллелепипед.

Полученный прямой параллелепипед подвергнем аналогичному преобразованию в прямоугольный параллелепипед, дополняя его сначала призмой 1, а затем отсекая призму 2 (рис. 476, б). Это преобразование также сохраняет объем параллелепипеда, площадь основания и высоту.

Объем прямоугольного параллелепипеда равен произведению его измерений. Произведение двух измерений есть площадь основания параллелепипеда, а третье измерение — его высота.

Таким образом, у прямоугольного параллелепипеда объем равен произведению площади основания на высоту. Так как при описанном выше преобразовании данного параллелепипеда в прямоугольный каждый раз сохраняются объем, площадь основания и высота, то и у исходного параллелепипеда объем равен произведению площади основания на высоту.

Итак, объем любого параллелепипеда равен произведению площади основания на высоту.
 

 

 
Задача (11). В прямом параллелепипеде стороны основания а и b образуют угол 30°. Боковая поверхность равна S. Найдите его объем.

Решение. Обозначим высоту через X (рис. 477). Тогда

(2a + 2b)x = S.

Отсюда

Площадь основания параллелепипеда равна аb . Объем равен

 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.