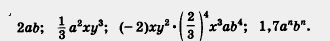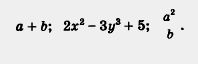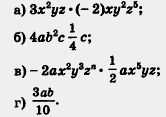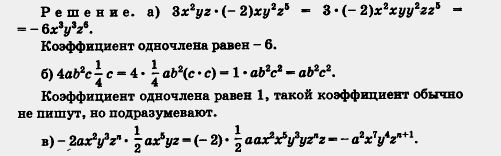|
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Понятие одночлена. Стандартный вид одночлена
Понятие одночлена. Стандартный вид одночлена.
Определение. Одночленом называют алгебраическое выражение, которое представляет собой произведение чисел и переменных, возведенных в степени с натуральными показателями.
Примеры одночленов:
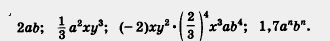
Одночленами считают также все числа, любые переменные, степени переменных. Например, одночленами являются:
0; 2; -0,6; х; a; b; x2; a3; bn.
Теперь приведем примеры алгебраических выражений, не являющихся одночленами:
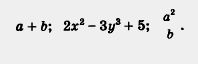
А как вы считаете: выражение — одночлен 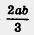 или нет? Ведь оно по форме похоже на выражение или нет? Ведь оно по форме похоже на выражение 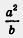 , которое фигурирует у нас в числе выражений, не являющихся одночленами, и содержит в своей записи черту дроби. Тем не менее — одночлен; чтобы убедиться в этом, , которое фигурирует у нас в числе выражений, не являющихся одночленами, и содержит в своей записи черту дроби. Тем не менее — одночлен; чтобы убедиться в этом,  . достаточно переписать —- в виде . достаточно переписать —- в виде 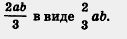 . .
Вот еще два примера, построенные на контрасте: 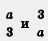 Как вы считаете, какое из этих выражений одночлен, а какое нет? А теперь проверьте себя: — Как вы считаете, какое из этих выражений одночлен, а какое нет? А теперь проверьте себя: — 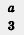 одночлен, его можно переписать в виде одночлен, его можно переписать в виде 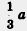 а; выражение а; выражение  же не является одночленом. Термины в математике надо употреблять правильно. же не является одночленом. Термины в математике надо употреблять правильно.
Рассмотрим одночлен 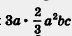 Глядя на это выражение, математик обычно думает так: «От перемены мест множителей произведение не изменится, перепишу-ка я это выражение в более удобном виде: Глядя на это выражение, математик обычно думает так: «От перемены мест множителей произведение не изменится, перепишу-ка я это выражение в более удобном виде:
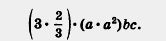
Тогда, — думает математик, — я получу 2a3bc, а эта запись приятнее той, что была, хотя бы потому, что короче. Кроме того, в ней нет того сумбура, какой был сначала: первый множитель — число, второй — переменная а, затем снова число, потом опять переменная а, но уже в квадрате и т. д.»
Стремящийся к четкости, краткости и порядку математик на самом деле привел одночлен к стандартному виду.
Вообще, чтобы привести одночлен к стандартному виду, нужно:
1) перемножить все числовые множители и поставить их произведение на первое место;
2) перемножить все имеющиеся степени с одним буквенным основанием;
3) перемножить все имеющиеся степени с другим буквенным основанием и т. д.
Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена
Любой одночлен можно привести к стандартному виду.
Пример. Привести одночлен к стандартному коэффициент виду и назвать коэффициент одночлена:
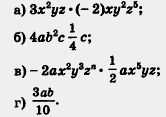
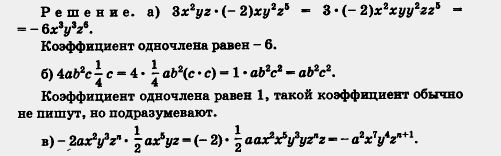
Коэффициент одночлена равен - 1.
г) А это, как говорят, «маленькая провокация»: одночлен не надо приводить к стандартному виду, он и так записан в стандартном виде. Коэффициент одночлена равен 0,3.
Планирование математике, материалы по математике 7 класса скачать, учебники онлайн
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|