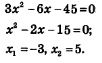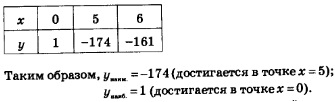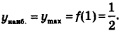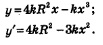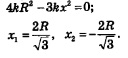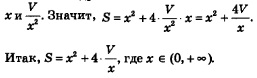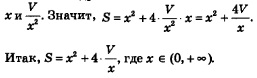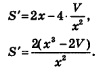Гипермаркет знаний>>Математика>>Математика 10 класс>> Применение производной для отыскания наибольших и наименьших значений величин

§ 36. Применение производной для отыскания наибольших и наименьших значений величин

1. Отыскание наибольшего и наименьшего значений непрерывной функции на промежутке Вы уже накопили некоторый опыт отыскания наибольшего и наименьшего значений функции. Чаще всего мы использовали для этого график функции. Пусть, например, дана функция
Построив ее график (см. рис. 143), легко сделать вывод о том, что
В некоторых случаях мы могли найти наибольшее и наименьшее значения функции и без помощи графика. Например, для функции можно рассуждать так: ясно, что (это значение достигается функцией в точке х=0). С другой стороны, ясно, что (это значение достигается функцией при х = 3 или при х = - 3).

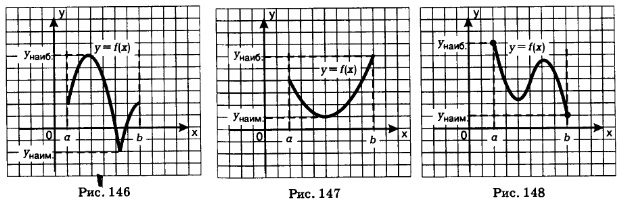
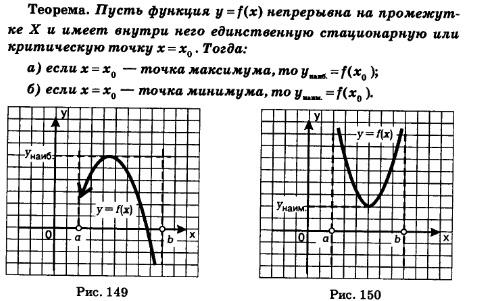
В более сложных случаях для отыскания наибольшего и наименьшего значений функции используется производная.

Пусть функция у = f(х) непрерывна на отрезке [а, 6] — несколько графиков таких функций представлено на рис. 146—148. Анализируя указанные геометрические модели, можно прийти к следующим выводам.

1.    Если функция непрерывна на отрезке, то она достигает на нем и своего наибольшего, и своего наименьшего значений.

Это — весьма солидная теорема курса математического анализа, доказательство ее требует достаточной продвинутости в изучении курса.

2.    Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.

Здесь возможны варианты — некоторые из них представлены на рис. 146—148. Смотрите: на рис. 146 и наибольшее, и наименьшее значения достигаются внутри отрезка. На рис. 147 наименьшее
значение достигается внутри отрезка, а наибольшее — в концевой точке. На рис. 148 и наибольшее, и наименьшее значения достигаются в концевых точках.

3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
В этом нет ничего удивительного, поскольку в этом случае наибольшее (или наименьшее) значение функции одновременно является экстремумом, а экстремум достигается только в стационарной или критической точке.
Подводя итог сказанному, нетрудно составить

Алгоритм отыскания наименьшего и наибольшего значения непрерывной функции  у = f(х) на отрезке [а, b]
1.    Найти производную f'(х).
2.    Найти стационарные и критические точки функции, лежащие внутри отрезка [а, Ь].
3.    Вычислить значения функции у = f(х) в точках, отобранных на втором шаге (п. 2), и в точках а и Ь; выбрать среди этих значений наименьшее (это и будет ) и наибольшее (это и будет ).

Алгоритм, как видите, сравнительно простой, для его иллюстрации достаточно одного примера. Мы приводим два примера, из которых второй — для тех, кому интересны математические «изюминки».

Пример 1. Найти наименьшее и наибольшее значения функции у = х³-Зх² -45х + 1:
а) на отрезке [-4, 6]; б) на отрезке [0, 6]; в) на отрезке [-2, 2].

Решение. Воспользуемся алгоритмом.

1)    Имеем у'= Зх² -6x-45.
2)    Производная существует при всех х, значит, критических точек у функции нет, а стационарные найдем из условия у'=0. Имеем:

Дальнейшие рассуждения зависят от условий задачи.
а) Обе стационарные точки (и х = - 3, и х = 5) принадлежат заданному отрезку [-4, 6]. Значит, на третьем шаге алгоритма мы составим такую таблицу значений функции у = х³ - Зх² -45х+1:

б) Отрезку [0, 6] принадлежит лишь одна из двух найденных стационарных точек, а именно точка х = 5. Значит, на третьем шаге мы составим такую таблицу значений функции у = х³ - Зх² - 45x: +1:

в) Отрезку [-2,2] не принадлежит ни одна из найденных стационарных точек, значит, достаточно вычислить значения функции в концевых точкахf(-2)= 71, f(2) =-93.
Таким образом, в этом случае
Пример 2. Найти наименьшее и наибольшее значения функции у = 5х³ - х|х-1| на отрезке [0, 2].
Решение. Если х>1, то |x-1|=x-1, и функция принимает вид: у = 5х"-х²+х; если х < 1, то |x-1|=1-x, и функция принимает вид у = 5х³ + х² - х. Таким образом, речь идет о кусочной функцииу = f(х) где

1)    Вычисляя f"(x)> мы должны учесть, что при х > 1 следует пользоваться формулой f(x) =5x³ ~х² +х. Получим: f'(х)=15х² -2х + 1.
При х < 1 следует пользоваться формулой f{х)=Ьх³ + х² -х. Получим f'(x) = 15x2 + 2х -1. В «точке стыка» х = 1 производная не существует, это — критическая точка функции.

2)    Критическую точку мы уже нашли — это точка х = 1. Найдем стационарные точки, решив уравнение f'(х)=0.
Если х > 1, то f'(x)=15x² -2x +1; уравнение 15x² -2x +1 =0 не имеет корней.
Если х < 1, то f'(x) = 15x² +2x-1; из уравнения 15x² +2x-1=0 находим: Из зтих двух значений заданному отрезку [0, 2] принадлежит только точка
3)    Составим таблицу значений функции у = 5x³ - х fх -11, включив в нее точки концы заданного отрезка и лежащие внутри отрезка критическую и стационарную точки.

Из имеющихся в таблице значений наименьшим является наибольшим 38.
Ответ:
А как быть, если речь идет об отыскании наибольшего или наименьшего значения функции, непрерывной на незамкнутом промежутке, например, на интервале? Можно построить график функции и снять информацию с полученной графической модели. Но чаще оказывается более удобным использовать следующую теорему.

На рис. 149 и 150 приведены соответствующие геометрические иллюстрации.
Пример 3. Найти наибольшее значение функции
Решение. (см- пример 7 из §35).
Производная всюду существует, значит, критических точек у функции нет.
Стационарные точки найдем из соотношения у'=0. Получаем: 1-х2 =0, откуда находим, что х=1 или х = -1. Заданному лучу [0, + принадлежит лишь точка х= 1. При х < 1 имеем у'> 0, а при х > 1 имеем у'<0. Значит, х= 1 — точка максимума функции, причем
Поскольку х = 1 — единственная точка экстремума функции на заданном промежутке, причем точка максимума, то, по теореме 1,

Ранее (см. рис. 143) был построен график функции на заданном луче — он хорошо иллюстрирует полученный результат.
Ответ:
2. Задачи иа отыскание наибольших и наименьших значений величин.

Российский математик XIX в. П.Л. Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды». С такими задачами в наше время приходится иметь дело представителям самых разных специальностей: инженеры-технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции; конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей; экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т.д.

Задачи подобного рода носят общее название — задачи на оптимизацию (от латинского слова орtimum — «наилучший»). В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависитют другой, причем надо найти такое значение второй величины, при котором первая принимает свое наименьшее или наибольшее (наилучшее в данных условиях) значение.  

Задачи на оптимизацию решают по обычной схеме из трех этапов математического моделирования: 1) составление математической модели; 2) работа с моделью; 3) ответ на вопрос задачи. Прежде чем переходить к конкретным примерам решения задач на оптимизацию, предлагаем некоторые рекомендации методического плана.

Первый зтап. Составление математической модели.

1) Проанализировав условия задачи, выделите оптимизируемую величину (сокращенно: О.В.), т.е. величину, о наибольшем или наименьшем значении которой идет речь. Обозначьте ее буквой у (или 8,У,В,1 — в зависимости от фабулы).

2)    Одну из участвующих в задаче неизвестных величин, через которую сравнительно нетрудно выразить О.В., примите за независимую переменную (сокращенно: Н.П.) и обозначьте ее буквой х (или какой-либо иной буквой). Установите реальные границы, изменения Н.П. (в соответствии с условиями задачи).

3)    Исходя из условий задачи, выразите у через х. Математическая модель задачи представляет собой функцию у = f(x) с областью определения X, которую нашли на втором шаге.

Второй этап. Работа с составленной моделью.

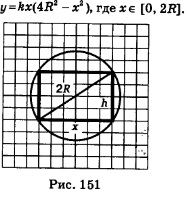
На этом этапе для функции в зависимости от того, что требуется в условии задачи. При этом используются теоретические установки, которые мы получили в п. 1 данного параграфа.

Третий этап. Ответ на вопрос задачи.

Здесь следует получить конкретный ответ на вопрос задачи, опираясь на результаты, полученные на этапе работы с моделью.

Пример 4. Прочность балки прямоугольного сечения пропорциональна произведению ее ширины на квадрат высоты. Какое сечение должна иметь балка, вытесанная из цилиндрического бревна радиуса Л, чтобы ее прочность была наибольшей?

Решение.

Первый этап. Составление математической модели.

1)    Оптимизируемая величина (О.В.) — прочность балки, поскольку в задаче требуется выяснить, когда прочность балки будет наибольшей. Обозначим О.В. буквой у.

2)    Прочность зависит от ширины и высоты прямоугольника, служащего осевым сечением балки. Объявим независимой переменной (Н.П.) ширину балки, обозначим ее буквой х. Поскольку осевое сечение представляет собой прямоугольник, вписанный в окружность радиуса В (рис. 151), то 0<х<2В (при х= 0 и при х=2В прямоугольник «вырождается» в отрезок, равный диаметру окружности) — таковы реальные
границы изменения независимой переменной.

3) Высота Н прямоугольника связана с его шириной соотношением х² + Н² =4В² (по теореме Пифагора). Значит, Н² =4В² - х².

А прочность балки у пропорциональна произведению (где коэффициент к — некоторое положительное число). Значит,

Математическая модель задачи составлена.

Второй этап. Работа с составленной моделью.

На этом этапе для функции Воспользуемся алгоритмом из п.1.
Имеем:

Приравняв производную нулю, получим:

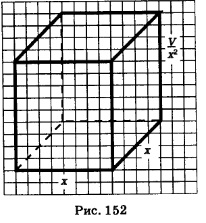
Заданному отрезку [0, 2R] принадлежит лишь точка х = x₁ Осталось вычислить значения функции в точке x, и на концах отрезка, т.е. в точках 0 и 2R.
Имеем:

Третий этап. Ответ на вопрос задачи.
В задаче спрашивается, какое сечение должна иметь балка наибольшей прочности. Мы выяснили, что ширина ж прямоугольника, служащего осевым сечением наиболее прочной балки, равна

  Найдем высоту:
Значит,

Ответ: Сечением балки должен служить прямоугольник, у которого отношение высоты к ширине равно
3 а м е ч а н и е. Квалифицированные мастера приходят к такому же результату, опираясь на свой опыт, но, разумеется, они принимают указанное отношение равным 1,4 (приближенное значение иррационального числа как раз равно 1,4).

Пример 5. Бак, имеющий вид прямоугольного параллелепипеда с квадратным основанием, должен вмещать V литров жидкости. При какой стороне основания площадь поверхности бака (без крышки) будет наименьшей?

Решение. Первый этап. Составление математической модели.

1)    Оптимизируемая величина (О.В.) — площадь поверхности бака, поскольку в задаче требуется выяснить, когда эта площадь |5удет наименьшей. Обозначим О.В. буквой 5.

2)    Площадь поверхности зависит от измерений прямоугольного параллелепипеда. Объявим независимой переменной (Н.П.) сторону квадрата, служащего основанием бака; обозначим ее буквой ж. Ясно, что x > 0. Других ограничений нет, значит, . Таковы реальные границы изменения независимой переменной.

3) Если h — высота бака, то V = х²h, откуда находим
На рис. 152 изображен прямоугольный параллелепипед, указаны его измерения. Поверхность бака состоит из квадрата со стороной х и четырех прямоугольников со сторонами

Математическая модель задачи составлена.

Второй этап. Работа с составленной моделью.

На этом этапе для функции
Для этого нужна производная функции. Имеем:

На промежутке критических точек нет, а стационарная точка только одна: S'= 0 при
Заметим, что при выполняется неравенство S'<0, а при выполняется неравенство S'>0. Значит, —единственная точка экстремума функции на заданном промежутке, а потому согласно теореме из п. 1, в этой точке функция достигает своего наименьшего значения.

Третий этап. Ответ на вопрос задачи.
В задаче спрашивается, какой должна быть сторона основания, чтобы бак имел наименьшую поверхность. Мы выяснили, что сторона квадрата, служащего основанием такого бака, равна 

Ответ:

А.Г. Мордкович Алгебра 10 класс

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.