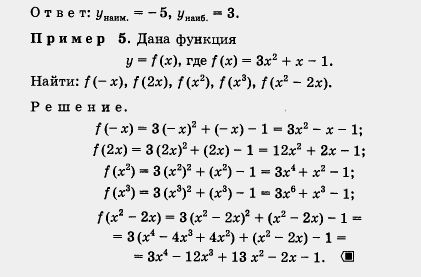|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Функция у = ах2 + bх + с, ее свойства и график
Функция у = ах2 + bх + с, ее свойства и график
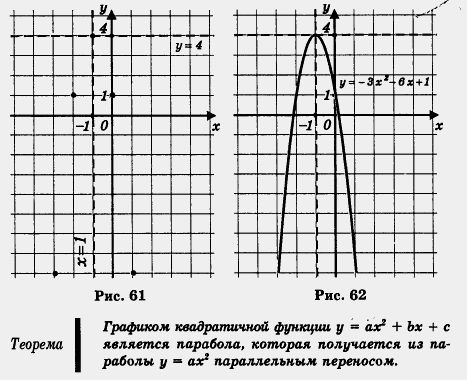
Функцию у = ах2 + bх + с, где а, b, с — произвольные числа, причем а Опираясь на результаты, полученные выше, мы с вами сможем построить график любой квадратичной функции. Один такой график мы построили в конце предыдущего параграфа, воспользовавшись методом выделения полного квадрата. Рассмотрим еще один пример. Пример 1. Построить график функции у = - bх2 - 6х + 1. Решение. Выделим полный квадрат в квадратном трехчлене -bх2 - 6х + 1. Имеем Для построения графика функции у = -3(х + I)2 + 4 перейдем к вспомогательной системе координат с началом в точке (-1; 4) (пунктирные прямые х = -1 и у = 4 на рис. 61). Привяжем функцию у = - Зх2 к новой системе координат. С этой целью выберем контрольные точки для функции у = - Зх2, например: (0; 0), (1; -3), (-1; -3), (2; -12), (-2; -12), но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 61). По этим точкам построим параболу — получим требуемый график (рис. 62). Итак, применив метод выделения полного квадрата, мы преобразовали квадратный трехчлен к виду а(х + I)2 + m и использовали алгоритм 2 из §12 (заметим, что с равным успехом мы могли бы использовать и алгоритм 1 — кому что нравится). Оказалось что графиком функции у = -Зх2- 6x = 1 является парабола которая получается из параболы у = -Зх2 параллельным переносом А в конце предыдущего параграфа мы установили, что графиком функции у = х2 - 4x+ 5 так же является парабола; она получается из параболы у = х2 параллельным переносом. Оказывается график любой квадратичной функции у = ах2+ bх + с можно получить из параболы у = ах2 параллельным переносом, причем для доказательства этого факта используется та же идея — выделение полного квадрата.
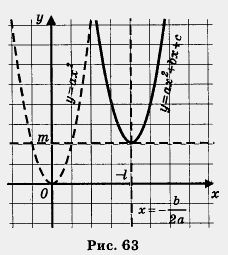
Чтобы построить график функции у = а(х + I)2 + m, нужно выполнить параллельный перенос параболы у = ах2 так, чтобы вершина параболы оказалась в точке (-l; m) (рис. 63). Теорема доказана.
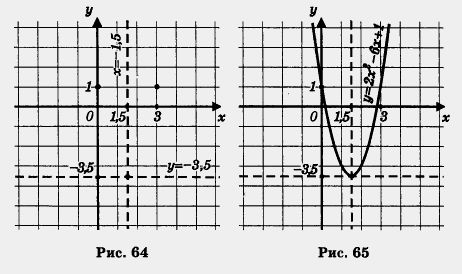
Во-первых, она довольно громоздкая, а во-вторых, если известна абсцисса х0, то ординату у0 всегда можно вычислить по формуле Пример 2. Не выполняя построения графика функции y = - 3x2 - 6 = 1 ответить на следующие вопросы: а) Какая прямая служит осью параболы? б) Каковы координаты вершины параболы? в) Куда (вверх или вниз) направлены ветви параболы? Решение, а) Здесь а = - 3, b = - 6. Уравнение оси параболы в) Парабола у = - 3х2 - 6х + 1 получается параллельным переносом параболы у = -Зх2. Ветви параболы у = -Зх2 направлены вниз (поскольку коэффициент при х2 отрицателен), значит, и у параболы у = - Зх2 - 6х + 1 ветви направлены вниз. Замечание. Сравните примеры 1 и 2. Речь в них идет об одной и той же параболе, но в примере 1 мы ее построили, а в примере 2 строить параболу было не нужно. Проверьте по рис. 62 правильность ответов на вопросы примера 2. Для любой функции вида у = ах2 + bх + с можно ответить на поставленные в примере 2 вопросы, не строя параболу — график функции. Легче всего ответить на вопрос, куда направлены ветви параболы: ветви параболы у = ах2 + bх + с направлены вверх, если а > 0, и вниз, если а < 0. Несколько сложнее найти уравнение оси параболы: Решение. Графиком функции является парабола с ветвями, направленными вверх, поскольку старший коэффициент 2 — положительное число. Найдем координаты вершины параболы. Имеем а = 2, b = -6;
На рис. 64 отмечена точка (1,5; - 3,5) — вершина искомой параболы, проведена ось параболы. Чтобы построить саму параболу, поступим так: возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = 0 и х = 3; вычислим значения функции в этих точках, учтя, что f (0) =f(3). Имеем f(0) = 1, значит, и f(3) = 1. Точки (0; 1) и (3; 1) отмечены на рис. 64. А теперь, зная три точки, построим искомую параболу (рис. 65)
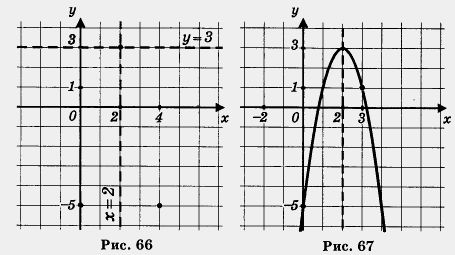
Алгоритм построения параболы у = ах2 + bх + с 1. Найти координаты вершины параболы, построить на координатной плоскости соответствующую точку, провести ось параболы. 2. Отметить на оси х две точки, симметричные относительно оси параболы (чаще всего в качестве одной из таких точек берут точку х = 0), найти значения функции в этих точках; построить на координатной плоскости соответствующие точки. 3. Через полученные три точки провести параболу (в случае необходимости берут еще пару точек, симметричных относительно оси параболы, и строят параболу по пяти точкам). Пример 4. Найти наименьшее и наибольшее значения функции у = - 2х2 + 8x - 5 на отрезке [0, 3]. Решение. Первый этап. Построим параболу, служащую графиком заданной функции. Воспользуемся алгоритмом. Значит, вершиной параболы служит точка (2; 3), а осью параболы — прямая х = 2 (рис. 66). 2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = 0 и х = 4. Имеем f(0) =f(4) = = -5; построим на координатной плоскости точки (0; - 5) и (4; - 5) (рис. 66). Второй этап. Выделим часть построенного графика на отрезке [0, 3]. Замечаем (см. выделенную часть параболы на рис. 67), что унаим. = - 5 (достигается при х = 0), а yнаиб. = 3 (достигается при х = 2). Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Книги и учебники согласно календарному плануванння по математике 8 класса скачать, помощь школьнику онлайн Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: