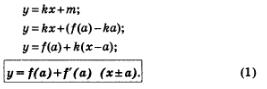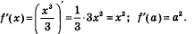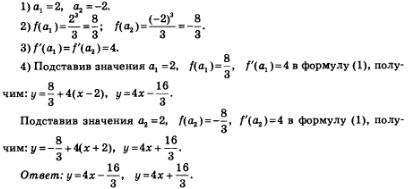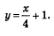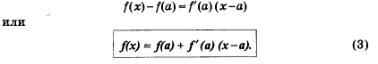|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Уравнение касательной к графику функции
§ 34. Уравнение касательной к графику функции
В § 32 говорилось о том, что если точка М (а; f(а)) принадлежит графику функции у = f(х) и если в этой точке к графику функции можно провести касательную, не перпендикулярную к оси абсцисс, то угловой коэффициент касательной равен f'(а). Мы этим уже несколько раз пользовались. Например, в § 33 было установлено, что график функции у = sin х(синусоида) в начале координат образует с осью абсцисс угол 45° (точнее, касательная к графику в начале координат составляет с положительным направлением оси х угол 45°), а в примере 5 § 33 были найдены точки на графике заданной функции, в которых касательная параллельна оси абсцисс. В примере 2 § 33 было составлено уравнение касательной к графику функции у = х2 в точке х = 1 (точнее, в точке (1; 1), но чаще указывают только значение абсциссы, полагая, что если значение абсциссы известно, то значение ординаты можно найти из уравнения у = f(х)). В этом параграфе мы выработаем алгоритм составления уравнения касательной.к графику любой функции.
Пусть даны функция у = f(х) и точка М (а; f(а)), а также известно, что существует f'(а). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид у = кх+m, поэтому задача состоит в отыскании значений коэффициентов к и m.
С угловым коэффициентом к проблем нет: мы знаем, что к = f'(а). Для вычисления значения т воспользуемся тем, что искомая прямая проходит через точку М(а; f (а)). Это значит, что, если подставить координаты точки М в уравнение прямой, получим верное равенство: f(а) = ка+m, откуда находим, что m = f(а) - ка.
Осталось подставить найденные значения коэффициентов кит в уравнение прямой:
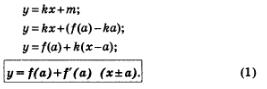
Нами получено уравнение касательной к графику функции у = f(х) в точке х=а.
Если, скажем, 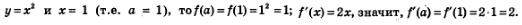
Подставив в уравнение (1) найденные значения а = 1, f(а) = 1 f'(а) = 2, получим: у = 1+2(х-f), т.е. у = 2х-1.
Сравните этот результат с тем, что был получен в примере 2 из § 33. Естественно, получилось то же самое.
Составим уравнение касательной к графику функции у = tg х в начале координат. Имеем: 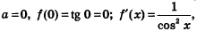 значит, соs х f'(0) = 1. Подставив в уравнение (1) найденные значения а= 0, f(а)= 0, f'(а) = 1, получим: у=х. значит, соs х f'(0) = 1. Подставив в уравнение (1) найденные значения а= 0, f(а)= 0, f'(а) = 1, получим: у=х.
Именно поэтому мы и провели тангенсоиду в § 15 (см. рис. 62) через начало координат под углом 45° к оси абсцисс.
Решая эти достаточно простые примеры, мы фактически пользовались определенным алгоритмом, который заложен в формуле (1). Сделаем этот алгоритм явным.
АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у = f(x)
1) Обозначить абсциссу точки касания буквой а.
2) Вычислить 1 (а).
3) Найти f'(х) и вычислить f'(а).
4) Подставить найденные числа а, f(а), (а) в формулу (1).
Пример 1. Составить уравнение касательной к графику функции 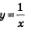 в точке х = 1. в точке х = 1.
Решение. Воспользуемся алгоритмом, учитывая, что в данном примере
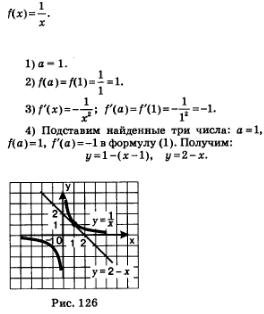
На рис. 126 изображена гипербола 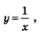 , построена прямая у= 2-х. , построена прямая у= 2-х.
Чертеж подтверждает приведенные выкладки: действительно, прямая у = 2-х касается гиперболы в точке(1; 1).
Ответ: у =2- х.
Пример 2. К графику функции 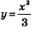 провести касательную так, чтобы она была параллельна прямой у =4х - 5. провести касательную так, чтобы она была параллельна прямой у =4х - 5.
Решение. Уточним формулировку задачи. Требование «провести касательную» обычно означает «составить уравнение касательной». Это логично, ибо если человек смог составить уравнение касательной, то вряд ли он будет испытывать затруднения с построением на координатной плоскости прямой по ее уравнению.
Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере 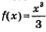 Но в отличие от предыдущего примера здесь имеется неясность: не указана явно абсцисса точки касания. Но в отличие от предыдущего примера здесь имеется неясность: не указана явно абсцисса точки касания.
Начнем рассуждать так. Искомая касательная должна быть параллельна прямой у = 4х-5. Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты. Значит, угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой: 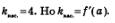 Таким образом, значение а мы можем найти из уравнения f'(а)= 4. Таким образом, значение а мы можем найти из уравнения f'(а)= 4.
Имеем: 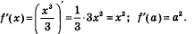
Из уравнения 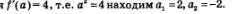 Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2. Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.
Теперь можно действовать по алгоритму.
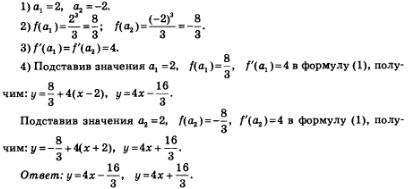
Пример 3. Из точки (0; 1) провести касательную к графику функции 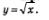
Решение. Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере 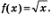 Заметим, что и здесь, как в примере 2, не указана явно абсцисса точки касания. Тем не менее действуем по алгоритму. Заметим, что и здесь, как в примере 2, не указана явно абсцисса точки касания. Тем не менее действуем по алгоритму.

По условию касательная проходит через точку (0; 1). Подставив в уравнение (2) значения х = 0, у = 1, получим: 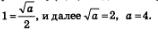
Как видите, в этом примере только на четвертом шаге алгоритма нам удалось найти абсциссу точки касания. Подставив значение а =4 в уравнение (2), получим:
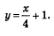
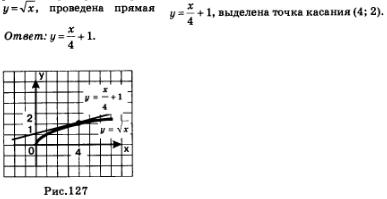
На рис. 127 представлена геометрическая иллюстрация рассмотренного примера: построен график функции
В § 32 мы отметили, что для функции у = f(х), имеющей производную в фиксированной точке х, справедливо приближенное равенство:
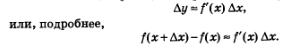
Для удобства дальнейших рассуждений изменим обозначения: вместо х будем писать а, вместо 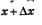 будем писать х и соответственно вместо будем писать х и соответственно вместо 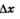 будем писать х-а. Тогда написанное выше приближенное равенство примет вид: будем писать х-а. Тогда написанное выше приближенное равенство примет вид:
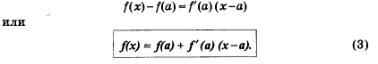
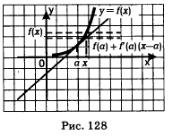
А теперь взгляните на рис. 128. К графику функции у = f(х) проведена касательная в точке М (а; f (а)). Отмечена точка х на оси абсцисс близко от а. Ясно, что f(х) — ордината графика функции в указанной точке х. А что такое f(а) + f'(а) (х-а)? Это ордината касательной, соответствующая той же точке х — см. формулу (1). В чем же смысл приближенного равенства (3)? В том, что для вычисления приближенного значения функции берут значение ординаты касательной.
Пример 4. Найти приближенное значение числового выражения 1,027.
Решение. Речь идет об отыскании значения функции у = х7 в точке х = 1,02. Воспользуемся формулой (3), учтя, что в данном примере 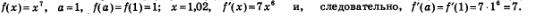
В итоге получаем:
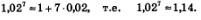
Если мы воспользуемся калькулятором, то получим: 1,027 = 1,148685667...
Как видите, точность приближения вполне приемлема.
Ответ: 1,027 =1,14.
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|