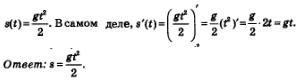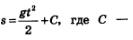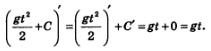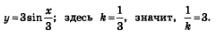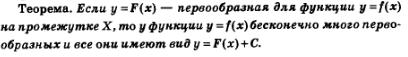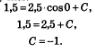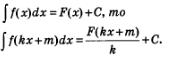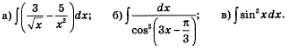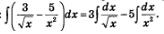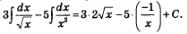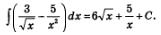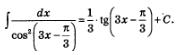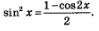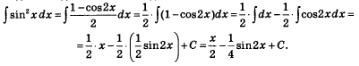|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Первообразная и неопределенный интеграл
§ 37. Первообразная и неопределенный интеграл
1. Первообразная
В предыдущих параграфах мы по заданной функции, руководствуясь различными формулами и правилами, находили ее производную. Мы убедились в том, что производная имеет многочисленные применения: производная — это скорость движения (или, обобщая, скорость протекания любого процесса); производная — это угловой коэффициент касательной к графику функции; с помощью производной можно исследовать функцию на монотонность и экстремумы; производная помогает решать задачи на оптимизацию.
Но в реальной жизни приходится решать и обратные задачи: например, наряду с задачей об отыскании скорости по известному закону движения встречается и задача о восстановлении закона движения по известной скорости. Рассмотрим одну из таких задач.
Пример 1. По прямой движется материальная точка, скорость ее движения в момент времени t задается формулой u = tg. Найти закон движения.
Решение. Пусть s = s(t) — искомый закон движения. Известно, что s'(t) = u"(t). Значит, для решения задачи нужно подобрать функцию s = s(t), производная которой равна tg. Нетрудно догадаться, что
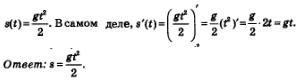
Сразу заметим, что пример решен верно, но неполно. Мы получили, что 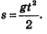 На самом деле, задача имеет бесконечно много решений: любая функция вида На самом деле, задача имеет бесконечно много решений: любая функция вида 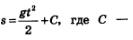 произвольная константа, может служить законом движения, поскольку произвольная константа, может служить законом движения, поскольку
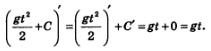
Чтобы задача стала более определенной, нам надо было зафиксировать исходную ситуацию: указать координату движущейся точки в какой-либо момент времени, например, при t=0. Если, скажем, s(0) = s0, то из равенства 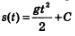 получаем s(0) = 0+С, т.е.S0 = С. Теперь закон движения определен однозначно: получаем s(0) = 0+С, т.е.S0 = С. Теперь закон движения определен однозначно: 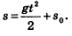
В математике взаимно обратным операциям присваивают разные названия, придумывают специальные обозначения: например, возведение в квадрат (х2) и извлечение квадратного корня 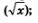 синус(sinх) и арксинус (аrcsin х) и т.д. Процесс отыскания производной по заданной функции называют дифференцированием, а обратную операцию, т.е. процесс отыскания функции по заданной производной — интегрированием. синус(sinх) и арксинус (аrcsin х) и т.д. Процесс отыскания производной по заданной функции называют дифференцированием, а обратную операцию, т.е. процесс отыскания функции по заданной производной — интегрированием.
Сам термин «производная» можно обосновать «по-житейски»: функция у - f(х) «производит на свет» новую функцию у'= f'(x)• Функция у = f(х) выступает как бы в качестве «родителя», но математики, естественно, не называют ее «родителем» или «производителем», они говорят, что это, по отношению к функции у'=f'(х), первичный образ, или, короче, первообразная.
Определение 1. Функцию у = F(х) называют первообразной для функции у = f(х) на заданном промежутке X, если для всех х из X выполняется равенство F'(х)=f(х).
На практике промежуток X обычно не указывают, но подразумевают ( в качестве естественной области определения функции).
Приведем примеры:
1) Функция у = х2 является первообразной для функции у = 2х, поскольку для всех х справедливо равенство (х2)' =2х.
2) функция у — х3 является первообразной для функции у-Зх2, поскольку для всех х справедливо равенство (х3)' = Зх2.
3) Функция у-sinх является первообразной для функции у=соsх, поскольку для всех х справедливо равенство (sinх)' =соsх.
4) Функция 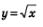 являетя первообразной для функции являетя первообразной для функции 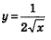 на промежутке на промежутке 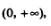 поскольку для всех х > 0 справедливо равенство поскольку для всех х > 0 справедливо равенство 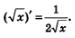
Вообще, зная формулы для отыскания производных, нетрудно составить таблицу формул для отыскания первообразных.
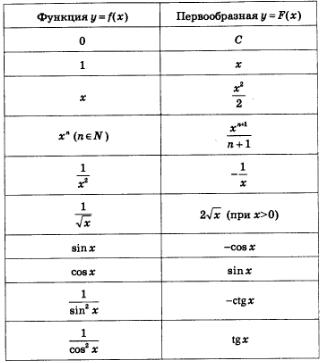
Надеемся, вы поняли, как составлена эта таблица: производная функции, которая записана во втором столбце, равна той функции, которая записана в соответствующей строке первого столбца (проверьте, не поленитесь, это очень полезно). Например, для функции у = х5 первообразной, как вы установите, служит функция 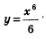 (см. четвертую строку таблицы). (см. четвертую строку таблицы).
Замечания: 1. Ниже мы докажем теорему о том, что если у = F(х) — первообразная для функции у = f(х), то у функции у = f(х)бесконечно много первообразных и все они имеют вид у = F(х) + С. Поэтому правильней было бы во втором столбце таблицы всюду добавить слагаемое С, где С — произвольное действительное число.
2. Ради краткости иногда вместо фразы «функция у = F(х) является первообразной для функции y = f(x)», говорят F(х) — первообразная для f(x)».
2. Правила отыскания первообразных
При отыскании первообразных, как и при отыскании производных, используются не только формулы (они указаны в таблице на с. 196), но и некоторые правила. Они непосредственно связаны с соответствующими правилами вычисления производных.
Мы знаем, что производная суммы равна сумме производных. Это правило порождает соответствующее правило отыскания первообразных.
Правило 1. Первообразная суммы равна сумме первообразных.
Обращаем ваше внимание на некоторую «легковесность» этой формулировки. На самом деле следовало бы сформулировать теорему: если функции у = f(х) и у=g{х) имеют на промежутке X первообразные, соответственно у-F(х) и у-G(х), то и сумма функций у = f(х)+g(х) имеет на промежутке X первообразную, причем этой первообразной является функция у = F(х)+G(х). Но обычно, формулируя правила (а не теоремы), оставляют только ключевые слова — так удобнее для применения правила на практике
Пример 2. Найти первообразную для функции у = 2х + соз х.
Решение. Первообразной для 2х служит х'; первообразной для созх служит sin х. Значит, первообразной для функции у=2х + соз х будет служить функция у = х2 + sin х (и вообще любая функция вида У = х1 + sinх + С).
Мы знаем, что постоянный множитель можно вынести за знак производной. Это правило порождает соответствующее правило отыскания первообразных.
Правило 2. Постоянный множитель можно вынести за знак первообразной.
Пример 3. Найти первообразные для заданных функций:
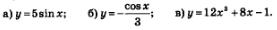
Ре ш е н и е. а) Первообразной для sin х служит -соз х; значит, для функции у = 5 sin х первообразной будет функция у = -5соз х.
б) Первообразной для соз x служит sin x; значит, для функции 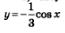 первообразной будет функция первообразной будет функция 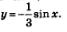
в) Первообразной для х3 служит 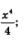 первообразной для х служит первообразной для х служит 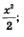 первообразной для функции у = 1 служит функция у = х. Используя первое и второе правила отыскания первообразных, получим, что первообразной для функции у = 12х3 + 8х-1 служит функция первообразной для функции у = 1 служит функция у = х. Используя первое и второе правила отыскания первообразных, получим, что первообразной для функции у = 12х3 + 8х-1 служит функция 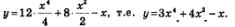
Замечание. Как известно, производная произведения не равна произведению производных (правило дифференцирования произведения более сложное) и производная частного не равна частному от производных. Поэтому нет и правил для отыскания первообразной от произведения или первообразной от частного двух функций. Будьте внимательны!
Получим еще одно правило отыскания первообразных. Мы знаем, что производная функции у = f(кх+m) вычисляется по формуле
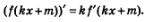
Это правило порождает соответствующее правило отыскания первообразных.
Правило 3. Если у = F(х) — первообразная для функции у = f(х), то первообразной для функции у=f(кх+m) служит функция
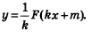
В самом деле,
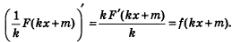
Это и означает, что 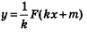 является первообразной для функции у = f(кх+m). является первообразной для функции у = f(кх+m).
Смысл третьего правила заключается в следующем. Если вы знаете, что первообразной для функции у = f(х) является функция у = F(х),а.вам нужно найти первообразную функции у = f(кх+m), то действуйте так: берите ту же самую функцию F, но вместо аргумента х подставьте выражение кх+m; кроме того, не забудьте перед знаком функции записать «поправочный множитель» 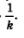
Пример 4. Найти первообразные для заданных функций:
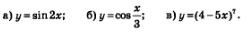
Решение, а) Первообразной для sin х служит -соз х; значит, для функции у = sin2х первообразной будет функция 
б) Первообразной для соз х служит sin х; значит, для функции 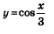 первообразной будет функция первообразной будет функция
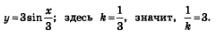
в) Первообразной для х7 служит 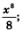 значит, для функции у=(4-5х)7 первообразной будет функция значит, для функции у=(4-5х)7 первообразной будет функция 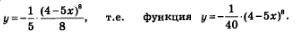
3. Неопределенный интеграл
Выше мы уже отмечали, что задача отыскания первообразной для заданной функции у = f(х)имеет не одно решение. Обсудим этот вопрос более детально.
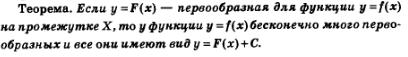
Доказательство. 1. Пусть у = F(х) — первообразная для функции у = f(х) на промежутке X. Это значит, что для всех х из X выполняется равенство x"(х) = f(х). Найдем производную любой функции вида у = F(х)+С:
(F(х) +С) = F'(х) +С = f(x) +0 = f(x).
Итак, (F(х)+С) = f(х). Это значит, что у = F(х) +С является первообразной для функции у = f(х).
Таким образом, мы доказали, что если у функции у = f(х) есть первообразная у=F(х), то у функции {f = f(x) бесконечно много первообразных, например, любая функция вида у = F(х)+С является первообразной.
2. Докажем теперь, что указанным видом функций исчерпывается все множество первообразных.
Пусть у=F1(х) и у=F(х) — две первообразные для функции У = f(x)на промежутке X. Это значит, что для всех х из промежутка X выполняются соотношения: F^ (х) = f(х); F'(х) = f(х).
Рaсмотрим функцию у = F1 (х) -.F(х) и найдем ее производную: (F, (х) -F(х))' = F[(х)-F(х) = f(х) - f(х) = 0.
Известно, что если производная функции на промежутке X тождественно равна нулю, то функция постоянна на промежутке X (см. теорему 3 из § 35). Значит, F1(х)-F(х) =С, т.е. Fх) = F(х)+С.
Теорема доказана.
Пример 5. Задан закон изменения скорости от времени v = -5sin2t. Найти закон движения s = s(t), если известно, что в момент времени t=0 координата точки равнялась числу 1,5 (т.е. s(t) = 1,5).
Решение. Так как скорость — производная координаты как функции от времени, то нам прежде всего нужно найти первообразную от скорости, т.е. первообразную для функции v = -5sin2t. Одной из таких первообразных является функция 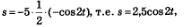 , а множество всех первообразных имеет вид: , а множество всех первообразных имеет вид:

Чтобы найти конкретное значение постоянной С, воспользуемся начальными условиями, согласно которым, s(0) = 1,5. Подставив в формулу (1) значения t=0, S = 1,5, получим:
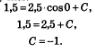
Подставив найденное значение С в формулу (1), получим интересующий нас закон движения:
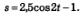
Определение 2. Если функция у = f(х) имеет на промежутке X первообразную у = F(х), то множество всех первообразных, т.е. множество функций вида у = F(х) + С, называют неопределенным интегралом от функции у = f(x) и обозначают:
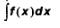
(читают: «неопределенный интеграл эф от икс дэ икс»).
В следующем параграфе мы выясним, в чем состоит скрытый смысл указанного обозначения.
Опираясь на имеющуюся в этом параграфе таблицу первообразных, составим таблицу основных неопределенных интегралов:

Опираясь на приведенные выше три правила отыскания первообразных, мы можем сформулировать соответствующие правила интегрирования.
Правило 1. Интеграл от суммы функций равен сумме интегралов этих функций:
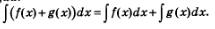
Правило 2. Постоянный множитель можно вынести за знак интеграла:
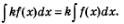
Правило 3. Если
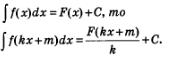
Пример 6. Найти неопределенные интегралы:
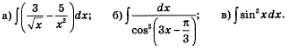
Решение, а) Воспользовавшись первым и вторым правилами интегрирования, получим:
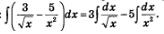
Теперь воспользуемся 3-й и 4-й формулами интегрирования:
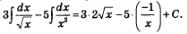
В итоге получаем:
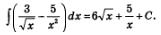
б) Воспользовавшись третьим правилом интегрирования и формулой 8, получим:
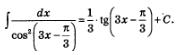
в) Для непосредственного нахождения заданного интеграла у нас нет ни соответствующей формулы, ни соответствующего правила. В подобных случаях иногда помогают предварительно выполненные тождественные преобразования выражения, содержащегося под знаком интеграла.
Воспользуемся тригонометрической формулой понижения степени:
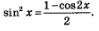
Тогда последовательно находим:
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|