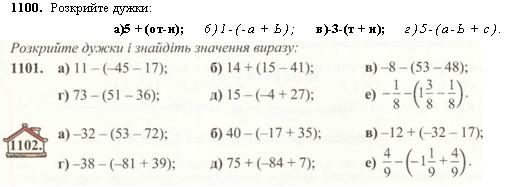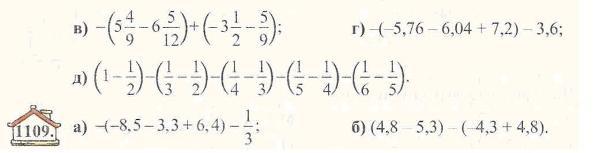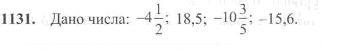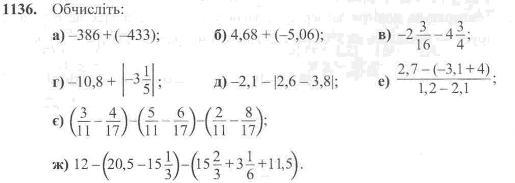Гіпермаркет Знань>>Математика>>Математика 6 клас>>Розкриття дужок

Ви вже знаєте, що на підставі сполучної властивості додавання вираз а+ (b+ с) можна записати без дужок:
а + (b + с)   =   a + Ь + с. Цю операцію називають розкриттям дужок. Оскільки b= +b, то останню рівність можна записати так:
а + (+b + с) =    а + b + с.

Ми розкрили дужки, перед якими стоїть знак «+». При цьому опустили лужки, знак «+», що стоїть перед ними, та записали всі доданки, які були в дужках, зі своїми знаками.

Отже, щоб розкрити дужки, перед якими стоїть знак «+», потрібно опустити дужки і знак «+», що стоїть перед ними, та записати всі доданки, які були в дужках, зі своїми знаками.

З цього правила випливають такі рівності:
а + (-b + с) = а -Ь + с; а + (b - с) = а + b - с, бо Ь = +b.
 
З правила віднімання раціональних чисел випливає, що
5 - (-7) = 5 + 7.

При виконанні цієї дії ми розкрили дужки, перед якими стоїть знак «-». При цьому опустили дужки та знак «-», що стоїть перед ними, і записали доданок, який був у дужках, з протилежним знаком. Так розкриватимемо дужки, перед якими стоїть знак «—» і тоді, коли доданків буде кілька:
а - (b + с) = а - (+b + с) = а - b - с.

Отже, щоб розкрити дужки, перед якими стоїть знак «-», по-трібно опустити дужки і знак «-», що стоїть перед ними, і запи-сати всі доданки, які були в дужках, із протилежними знаками.

Скориставшись цим правилом, матимемо:
а — (Ь — с) = а — (+b - с) = а - b + с.

Прочитайте
1.    Спростити вираз: m + 3 - (m - n + 4).
m + 3 - (m -n + 4) -m + 3 - m + n - 4 =
= (m-m) + n + (3-4) = 0 + n + (-1) = n-1.

2.    Узяти два останні доданки в дужки, поставивши перед дужками знак «+»,
у виразі: а)-1,2-4,1 + 3; б) -А + 5,3 - 2,1.

а)-1,2-4,1 + 3 =-1,2+ (-4,1 + 3).

Після першого доданка поставили знак «+», відкрили дужки, два останні доданки переписали з тими самими знаками і закрили дужки, б)-4+ 5,3-2,1 =^1 +(5,3-2,1).

(Перед першим доданком у дужках знак «+» можна не ставити.)

3.    Узяти два останні доданки в дужки, поставивши перед дужками знак «-», у виразі: а) 3-4,2+ 3,7; б) -10 + 7 -4,2.
а) 3 - 4,2 + 3,7 = 3 - (4,2 - 3,7).

Після першого доданка поставили знак «-», відкрили дужки, знак «-» у доданку ^1,2 змінили на «+», але не написали, оскільки у дужках цей доданок перший; у доданку +3,7 знак «+» змінили на «-».
б)-10+ 7-4,2 = -10-(-7+ 4,2).
 
Усно
1099.   Чи правильно розкрито дужки?
а) 3 + (-5 - 2) = 3 - 5 - 2;    б) 3 - (5 - 2) = 3 - 5 - 2;
в) 3 - (-5 + 2) = 3 + 5 - 2;    г) 3 - (5 + 2) = 3 - 5 + 2.

Рівень А

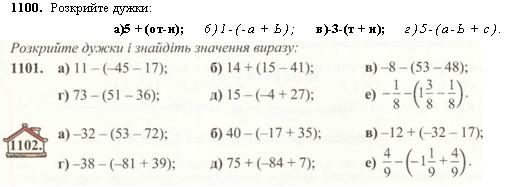
1103.   а)-(59-75)-(34-49);    б) (82 - 9) + (32 - 8);
в) (49 - 5) - (29 - 4);    г) -(8 - 102) - (142 - 53).

Розкрийте дужки і спростіть вираз:
1104.   а) 9-(а+ 37);    б) -(4 - а + 2) - 118;
в) Ь + (78 - Ь - 19);    г) -(а + 51) - (-а - 49).
 
1105.
а) -24 - (56 - а);    б) 41 - (52 + Ь - 15);
в) - (-5 + а) - 72;    г) - {а - 6) + (42 + а - 58).
 

Рівень Б
1106.   Спростіть вираз а + Ь - (Ь - с) + сі і знайдіть його значення, якщо а = -3,1; Ь = 0,017; с = -0,2; <І=-5.
 
1107.   Спростіть вираз а - b + (Ь - с) + 1,8 і знайдіть його значення, якщо а = 0.2; і = -0.35: с = -3.
 
Розкрийте дужки і знайдіть значення виразу:
1108.   а) (-3,5+ 7,6)-(10,8-8,3);    б) 85 - (3,17 + 4,6 - 5,8);
 

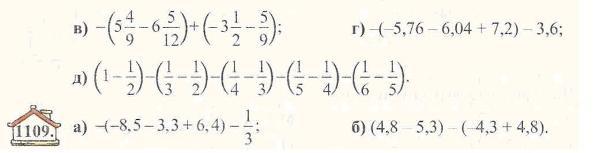
1110.    Запишіть суму виразів і спростіть її:
а) -5 + а і -а + 2,3;    б) 0,35 + т і -4.4 - т - 2,65;
в)а - b і b - а;    т)а -b+ b - а + 3.

1111.    Запишіть різницю виразів і спростіть її:
а) с + 17,1 і 8,5 + с;     б) -а + b і b - а;
в)а + b і b + с;             г)-а + b + k і b-а-2.

Розв'яжіть рівняння, спростивши спочатку вираз у лівій частині:
1112.    а) 4,8- (5,8 +х)= 1,2;    б) (х + 7,2) - 14 = 2,3;
            в}-9+(14,7-x)= 1,3;      г) -(х - 1,9)- 15 = 14,1.
 

1113. а) 8,3 - (-3,2 + х) = 12;    б) -(х - 2,25) + 4,88 = 1,3.
 
Візьміть у дужки два останні додагіки, поставивши перед дужками знак «+»; знак «—»:
1114.   а) -4+ 3 -7;       б) 6-а+5;    в)8-а + 6;    г)5 - а -b.
 
1115.    а) 5+ 8-3;        6)7-а + Ь;    в)а-5 + Ь;    т)-4 + а + b.
 
Здогадайтеся
1116. Щоденно опівдні з порту А до порту В і з порту В до порту А, вирушають пароплави. Рейси всіх пароплавів тривають 10,5 діб. Скільки пароплавів зустрічає за час рейсу кожний із цих пароплавів?

Вправи для повторення
1117.   Периметр трикутника АВС дорівнює 15 см. Довжина сторони АВ становить 44% периметра, а довжина сторони ВС становить — довжини сторони АВ. Яка довжина сторони АС?

1118.    У парку росте 450 дерев. Липи становлять — кількості всіх дерев і 80% кількості осик. Скільки лип і осик разом росте в парку?

1119.    Водій мав перевести вантаж з міста А до міста В, відстань між якими дорівнює ! 80 км. Він планував їхати 3 години й о 10 год ранку бути в місті В. Однак водій виїхав із запізненням і, щоб прибути до міста В вчасно, збільшив заплановану швидкість на 20%. О котрій годині водій виїхав з міста А?

1120.    Відстань між пунктами А і В дорівнює 60 км, до того ж, — шляху припадає на шосе, а решта — на ґрунтову дорогу. Мотоцикліст проїхав шлях між цими пунктами, рухаючись шосе зі швидкістю 40 км/год, а ґрунтовою дорогою — удвічі повільніше. Скільки часу їхав мотоцикліст?

Пам'ятка до §5

Запитання для самоперевірки і повторення
1.    Що таке координатна пряма?
2.    Де на координатній прямій розміщені точки, які відповідають додатним числам; від'ємним числам?
3.    Які числа називають протилежними?
4.    Які числа називають цілими; раціональними?
5.    Чому дорівнює модуль додатного числа; від'ємного числа; нуля?
6.    Як порівнювати числа за допомогою координатної прямої?
7.    Яке число більше: додатне чи від'ємне?
8.    Яке із двох від'ємних чисел більше?
9.    Як додати два від'ємні числа?
10.    Як додати два числа з різними знаками?
11.    Як виконати дію віднімання?
12.    Як розкрити дужки, перед якими стоїть знак «+»?
13.    Як розкрити дужки, перед якими стоїть знак «-»?

Завдання для повторення §5

1126.    Розв'яжіть рівняння:
а) |х| + 4 = 9;       б)|х|-1 = ^;       в) 10-И = 3,5;     г)2|х|-4 = 6.

1127.    Запишіть три значення х, що задовольняють умови:
а)х<0і|х|>5;    б)х<0і|х|<4.

Вкажіть одне число, яке:
1    2
1128.    менше від -—, але більше від -—.
1129.    менше від -3,3, але більше від -3,4.

1130.    На координатній прямій позначте точки, координати яких задовольняють умову:
а)-2<х<2;    б)-2,5<х<-1;    в)|х|<1,5.
Запишіть усі цілі числа, які задовольняють кожну нерівність.

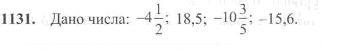
а)    Від суми перших двох чисел відніміть суму решти чисел.
б)    Від першого числа відніміть суму трьох останніх.
в)    Від різниці перших двох чисел відніміть різницю третього і четвертого.
г)    До різниці першого і четвертого чисел додайте суму другого і третього.

1132.   Знайдіть за допомогою координатної прямої суму чисел:
а)-3 і 4;    б)-5 і-2;    в)-8 ІЗ.

1133.    Дано числа: 14; -6; -11; -1,2. Запишіть кожне з них у вигляді: а) суми двох різних чисел;    б) різниці двох чисел.

1134.    Запишіть суму числа а і числа, протилежного числу Ь. Обчисліть цю суму, якщо а = -21, Ь = 9.

1135.    Запишіть суму числа а і числа, протилежного числу -Ь. Обчисліть цю суму, якщо а = 17, Ь = -11.

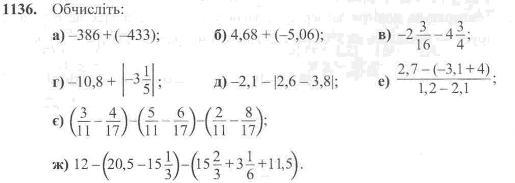
1137.   Розкрийте дужки і знайдіть значення виразу:
а) 4,35 -5-(1,63 - 2,72);    б) (0,211 + 0,817) - (0,302 -0,7).

1138:  Спростіть вираз: а) -5,3 + а + 7,2 + (-1,8);    б) b + 8,3 + (-14,2) +11-6;
                                     в) а - (а + Ь) + (b - с);        г)  -m+(m-n)-(k+a).
1139.   Візьміть у дужки три останні доданки, поставивши перед дужками знак
«+»; знак «-»:
а) 5-2+ 3-7-3,2;    6)4 + 5-7-9+14.

Розв 'яжіть рівняння:
(1140) а)5+х = -7,8;    б)4-х = -1,2;    в) 11-х- 8 =-2,3;
           г)-х + 7-18 = 5;    д)(х + 7)-11 =-8;        е) 14 - (х + 9) =-21.

1141.    а)|х| = 2,7;                 б)|х + 9| = 3;              в)|х-1| = 0;
            г)|х + 5| = -2;              д)|2-х| = 7;                е) |3,5-х| = 10.

1142.    Модуль суми чисел а і 5 дорівнює 0. Знайдіть а.

1143.    На координатній прямій позначте деяку точку А(а) і точки В(а + 3); С(а - 2); 0(а - 1,5).

1144.    На координатній прямій точка/1 відповідає числу о + 3, а точка В — числу а - 3. Якому числу відповідає середина відрізка?

1145.    Знайдіть відстань між точками А(х) і В(у), якщо:
а)х = -3;у = 2;    б)х = 5;_у = -4;    в)х = -2;у = -7.

1146.    На координатній прямій позначте точку А(2) і таку точку В, щоб довжина відрізка АВ дорівнювала 5 одиницям. Знайдіть координату точки В. Скільки може бути таких точок?

1147.    Відстань між точками А(х) і В(-А) дорівнює 7 одиницям. Знайдіть координату точки А. Скільки може бути таких координат?

1148 . Знайдіть три цілі числа, які задовольняють таким трьом умовам: 1) модуль кожного із чисел менший від 4; 2) сума двох найбільших чисел дорівнює 3; 3) сума двох найменших чисел дорівнює -1.

1149. Температура повітря за першу половину дня підвищилась на 6°С, а за другу — знизилась на 3°С. Як змінилась температура повітря за день?
 
Завдання для самоперевірки
1.       Запишіть числа, протилежні числам: 4; 0; -2.
 
2.       Порівняйте числа -5 і 2.
а)-5>2;    б)-5<2;
в) -5 = 2.
 
3.    Знайдіть модуль числа -7.
а)|-7|=-7;    ®|-7| = 7;    в)|-7| = 0.

4.    Знайдіть суму чисел -15 і +8.
а)-7;    б)-23;    в) 7;    г)23.

5.    Обчисліть:-8+ (-15).
а) 7;    6)23;    в)-7;     г)-23

6.    Знайдіть різницю чисел -11 і +8.
(а)-3;    6)-19;    в) 3;    г) 19.

ІІ рівень
7.       Знайдіть значення виразу -27 + 40 - (-11).
8.       Розкрийте дужки та знайдіть значення виразу -37 - (15 - 23).
9.       Розкрийте дужки та спростіть вираз (14-а)- (-21-а).

ІІІ рівень
10.      Знайдіть значення виразу:
а)-2,9+ 1,8 + (-11,1)-|-7,2|
6) -5,4-(-10-5,4+ 4,7)
 
11.      Розв'яжіть рівняння: а) 7,3 - х = -1,2;
б) (х+ 1,2)-1,9 = -2,4.
 
12.      Знайдіть відстань між точками л (-4) і В{ 11).
 
IV рівень
13.      На координатній прямій позначте точки, координати яких задовольняють

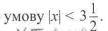
15.      Відстань між точками С(х) і £>(3) дорівнює 6 одиниць. Знайдіть координату точки С. Скільки розв'язків має задача?

Математика 6 клас Галина Янченко, Василь Кравчук

Вислано читачами iнтернет-сайту

_{Онлайн-бібліотека з підручниками і книгами, тести з математики, завдання з математики 6 клас, календарне планування}

 конспект уроку і опорний каркас                      
 презентація уроку 
 акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями)
 оцінювання 

Практика
 задачі та вправи,самоперевірка 
 практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання 

Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати
 фішки для допитливих
 шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати

Доповнення
 зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні 
 тематичні свята, девізи 
 статті 
 національні особливості
 словник термінів                          
 інше 

Тільки для вчителів
 ідеальні уроки 
 календарний план на рік 
 методичні рекомендації 
 програми
 обговорення

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.